ｽﾋﾟｷトルグラフ理論

あ、ｽﾋﾟｷだ。

この本に興味があるの？

$e(X,Y)=p|X||Y|+o(n^2)$ for all $X,Y\subseteq V(G)$

ｽﾋﾟｷには難しい本かもね。

気になる？

この本はスペクトルグラフ理論の本だよ。グラフの性質を行列の固有値を使って調べる分野なんだ。

今読んでいる部分はグラフのランダム性についてだよ。この条件はグラフがランダムっぽいことを定義してる。

ランダムグラフというのは、頂点と頂点の間に確率 $p$ で辺を張ることでできるグラフ。

試しに、このグラフにランダムに辺を描いてみて。

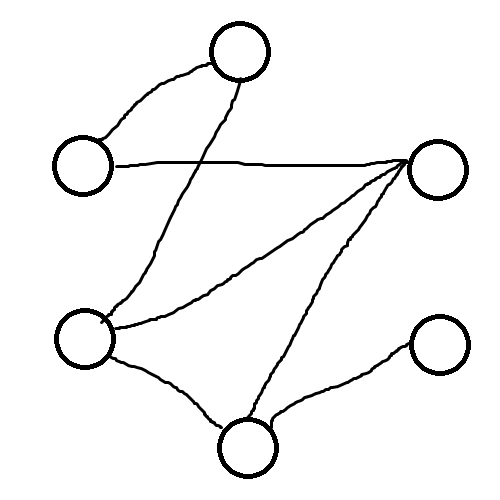
できたね。こういうのがランダムグラフ。

じゃあ、グラフがランダムっぽいことを確かめるにはどうしたらいいかな。

さっきの定義

$e(X,Y)=p|X||Y|+o(n^2)$ for all $X,Y\subseteq V(G)$

を使ってもいいけど、すべての $X,Y$ について確かめないといけないからこれは大変。

でも、固有値を使うとすごいことが起きる。実は次の条件と同値になるんだよ。

$\lambda_1\ge\lambda_2\ge\cdots\ge\lambda_n$ をグラフの隣接行列の固有値とするとき、$\lambda_1=pn+o(n)$ かつ $\max_{i\ne 1}|\lambda_i|=o(n)$

固有値を使ってグラフの性質を調べられるなんてすごいよね。

聞いてくれてありがとう。お礼にこれをあげるね。

参考文献

Zhao, Yufei. Graph theory and additive combinatorics. Cambridge University Press. (2023).

このおはなしはトリッカルの二次創作です。今すぐプレイ！

📢伝説ペット「ｽﾋﾟｷ」がまもなく登場❣️

目に涙を浮かべたスピッキーを模して作ったぬいぐるみ。なでると、おもちゃの笛みたいな音が鳴る。その音色は、スピッキーの泣き声にそっくりだという。

💝開催予定のイベントに参加すると、無料でゲットできるチャンスが🆓‼️
教主様、どうぞお楽しみに！… pic.twitter.com/v1zSLE3OED

— トリッカル・もちもちほっペ大作戦 (@trickcal_jp) December 28, 2025