月刊組合せ論 Natori は面白そうな組合せ論のトピックを紹介していく企画です。今回はフック長公式の q 類似を扱います。
7 月はヤング図形強化月間としていたので、ヤング図形に関する文献をたくさん読んでいました。やはりヤング図形はいいですね。
フック長公式(復習)
#
フック長公式は以下の記事で解説しています。
【月刊組合せ論 Natori】フック長公式【2023 年 5 月号】
ヤング図形 λ \lambda λ λ \lambda λ 1 , 2 , … , n 1,2,\ldots,n 1 , 2 , … , n n = ∣ λ ∣ n=|\lambda| n = ∣ λ ∣
λ \lambda λ f λ f^{\lambda} f λ
f λ = n ! ∏ □ ∈ λ h λ ( □ )
f^{\lambda}=\frac{n!}{\prod_{\square\in\lambda} h_{\lambda}(\square)}
f λ = ∏ □ ∈ λ h λ ( □ ) n ! ここで h λ ( □ ) h_{\lambda}(\square) h λ ( □ ) □ \square □
q 類似を考える
#
正整数 n n n q q q [ n ] q = 1 − q n 1 − q [n]_q=\frac{1-q^n}{1-q} [ n ] q = 1 − q 1 − q n n ! n! n ! q q q [ n ] q ! = [ 1 ] q [ 2 ] q ⋯ [ n ] q [n]_q!=[1]_q[2]_q\cdots [n]_q [ n ] q ! = [ 1 ] q [ 2 ] q ⋯ [ n ] q q → 1 q\to 1 q → 1 q q q
順列の場合、転倒数や major index といった statistics があります。これらを用いた母関数を考えると
∑ p ∈ S n q i n v ( p ) = ∑ p ∈ S n q m a j ( p ) = [ n ] q !
\sum_{p\in S_n}q^{\mathrm{inv}(p)}=\sum_{p\in S_n}q^{\mathrm{maj}(p)}=[n]_q!
p ∈ S n ∑ q inv ( p ) = p ∈ S n ∑ q maj ( p ) = [ n ] q ! が成り立ちます。このように、q q q
以下の記事もご覧ください。
【月刊組合せ論 Natori】Mahonian statistics【2024 年 10 月号】
タブローの statistics
#
タブローの statistics を 2 つ紹介します。
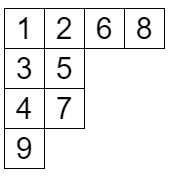
まず、タブロー T T T D e s ( T ) \mathrm{Des}(T) Des ( T ) i i i i + 1 i+1 i + 1 i i i
の場合、降下点集合は { 2 , 3 , 6 , 8 } \{2,3,6,8\} { 2 , 3 , 6 , 8 }
そして m a j ( T ) = ∑ i ∈ D e s ( T ) i \mathrm{maj}(T)=\sum_{i\in\mathrm{Des}(T)}i maj ( T ) = ∑ i ∈ Des ( T ) i
次に、タブロー T T T i < j i<j i < j j j j i i i ( i , j ) (i,j) ( i , j ) i n v ( T ) \mathrm{inv}(T) inv ( T )
いよいよ、q q q
∑ T ∈ S Y T ( λ ) q m a j ( T ) ∑ T ∈ S Y T ( λ ) q i n v ( T )
\begin{gather*}
\sum_{T\in\mathrm{SYT}(\lambda)}q^{\mathrm{maj}(T)} \\
\sum_{T\in\mathrm{SYT}(\lambda)}q^{\mathrm{inv}(T)}
\end{gather*}
T ∈ SYT ( λ ) ∑ q maj ( T ) T ∈ SYT ( λ ) ∑ q inv ( T ) を考えます。順列の場合と異なり、この 2 つは異なります。
よい公式は maj の場合しか知られていないそうです。
定理 : b ( λ ) = ∑ i ( i − 1 ) λ i b(\lambda)=\sum_i (i-1)\lambda_i b ( λ ) = ∑ i ( i − 1 ) λ i
∑ T ∈ S Y T ( λ ) q m a j ( T ) = q b ( λ ) [ n ] q ! ∏ □ ∈ λ [ h λ ( □ ) ] q
\sum_{T\in\mathrm{SYT}(\lambda)}q^{\mathrm{maj}(T)}=\frac{q^{b(\lambda)}[n]_q!}{\prod_{\square\in\lambda}[h_{\lambda}(\square)]_q}
T ∈ SYT ( λ ) ∑ q maj ( T ) = ∏ □ ∈ λ [ h λ ( □ ) ] q q b ( λ ) [ n ] q ! が成り立つ。
証明の鍵となるのは、シューア関数と fundamental quasisymmetric function (Gessel quasisymmetric function ともいう) です。S S S { 1 , 2 , … , n − 1 } \{1,2,\ldots,n-1\} { 1 , 2 , … , n − 1 }
L S = ∑ i 1 ≤ i 2 ≤ ⋯ ≤ i n i j < i j + 1 if j ∈ S x i 1 x i 2 ⋯ x i n
L_S=\sum_{\substack{i_1\le i_2\le\cdots\le i_n \\ i_j<i_{j+1} \text{ if } j\in S}}x_{i_1}x_{i_2}\cdots x_{i_n}
L S = i 1 ≤ i 2 ≤ ⋯ ≤ i n i j < i j + 1 if j ∈ S ∑ x i 1 x i 2 ⋯ x i n を fundamental quasisymmetric function といいます。このとき
s λ = ∑ T ∈ S Y T ( λ ) L D e s ( T )
s_{\lambda}=\sum_{T\in \mathrm{SYT}(\lambda)}L_{\mathrm{Des}(T)}
s λ = T ∈ SYT ( λ ) ∑ L Des ( T ) が成り立ちます。この式は今回は認めることにします。いつかこの式を解説する記事を書くかもしれません。
特殊値を計算しましょう。
L S ( 1 , q , q 2 , … ) = ∑ q ( i 1 − 1 ) + ( i 2 − 1 ) + ⋯ + ( i n − 1 )
L_S(1,q,q^2,\ldots)=\sum q^{(i_1-1)+(i_2-1)+\cdots+(i_n-1)}
L S ( 1 , q , q 2 , … ) = ∑ q ( i 1 − 1 ) + ( i 2 − 1 ) + ⋯ + ( i n − 1 ) を計算します。例えば S = { 1 , 3 } S=\{1,3\} S = { 1 , 3 } i 1 < i 2 ≤ i 3 < i 4 i_1<i_2\le i_3<i_4 i 1 < i 2 ≤ i 3 < i 4 r 1 = i 1 − 1 , r 2 = i 2 − 2 , r 3 = i 3 − 2 , r 4 = i 4 − 3 r_1=i_1-1, r_2=i_2-2, r_3=i_3-2, r_4=i_4-3 r 1 = i 1 − 1 , r 2 = i 2 − 2 , r 3 = i 3 − 2 , r 4 = i 4 − 3 0 ≤ r 1 ≤ r 2 ≤ r 3 ≤ r 4 0\le r_1\le r_2\le r_3\le r_4 0 ≤ r 1 ≤ r 2 ≤ r 3 ≤ r 4 j ∈ S j\in S j ∈ S j ∉ S j\not\in S j ∈ S r j r_j r j i j i_j i j
L S ( 1 , q , q 2 , … ) = ∑ 0 ≤ r 1 ≤ r 2 ≤ ⋯ ≤ r n q r 1 + ⋯ + r n + e ( S )
L_S(1,q,q^2,\ldots)=\sum_{0\le r_1\le r_2\le\cdots\le r_n} q^{r_1+\cdots+r_n+e(S)}
L S ( 1 , q , q 2 , … ) = 0 ≤ r 1 ≤ r 2 ≤ ⋯ ≤ r n ∑ q r 1 + ⋯ + r n + e ( S ) となります。ここで e ( S ) = ∑ j ∈ S ( n − j ) e(S)=\sum_{j\in S}(n-j) e ( S ) = ∑ j ∈ S ( n − j )
L S ( 1 , q , q 2 , … ) = q e ( S ) ( 1 − q ) ( 1 − q 2 ) ⋯ ( 1 − q n )
L_S(1,q,q^2,\ldots)=\frac{q^{e(S)}}{(1-q)(1-q^2)\cdots(1-q^n)}
L S ( 1 , q , q 2 , … ) = ( 1 − q ) ( 1 − q 2 ) ⋯ ( 1 − q n ) q e ( S ) がわかります。これを先ほどの等式に代入すると
s λ ( 1 , q , q 2 , ⋯ ) = ∑ T ∈ S Y T ( λ ) q c o m a j ( T ) ( 1 − q ) ( 1 − q 2 ) ⋯ ( 1 − q n )
s_{\lambda}(1,q,q^2,\cdots)=\frac{\sum_{T\in \mathrm{SYT}(\lambda)}q^{\mathrm{comaj}(T)}}{(1-q)(1-q^2)\cdots(1-q^n)}
s λ ( 1 , q , q 2 , ⋯ ) = ( 1 − q ) ( 1 − q 2 ) ⋯ ( 1 − q n ) ∑ T ∈ SYT ( λ ) q comaj ( T ) が得られます。ここで c o m a j ( T ) = ∑ j ∈ D e s ( T ) ( n − j ) \mathrm{comaj}(T)=\sum_{j\in\mathrm{Des}(T)}(n-j) comaj ( T ) = ∑ j ∈ Des ( T ) ( n − j )
左辺を別の方法で計算します。以下の記事の結果を用います。
【月刊組合せ論 Natori】半標準ヤングタブローの個数【2024 年 5 月号】
次の公式を証明していました。
s λ ( 1 , q , q 2 , … , q n − 1 ) = ∏ 1 ≤ i < j ≤ n q λ j + n − j − q λ i + n − i q i − 1 − q j − 1
s_{\lambda}(1,q,q^2,\ldots,q^{n-1})=\prod_{1\le i<j\le n}\frac{q^{\lambda_j+n-j}-q^{\lambda_i+n-i}}{q^{i-1}-q^{j-1}}
s λ ( 1 , q , q 2 , … , q n − 1 ) = 1 ≤ i < j ≤ n ∏ q i − 1 − q j − 1 q λ j + n − j − q λ i + n − i 上記の記事では q → 1 q\to 1 q → 1
s λ ( 1 , q , q 2 , … , q n − 1 ) = q b ( λ ) ∏ □ ∈ λ [ n + c ( □ ) ] q [ h λ ( □ ) ] q
s_{\lambda}(1,q,q^2,\ldots,q^{n-1})=q^{b(\lambda)}\prod_{\square\in\lambda}\frac{[n+c(\square)]_q}{[h_{\lambda}(\square)]_q}
s λ ( 1 , q , q 2 , … , q n − 1 ) = q b ( λ ) □ ∈ λ ∏ [ h λ ( □ ) ] q [ n + c ( □ ) ] q がわかります。いま n → ∞ n\to\infty n → ∞ ( 1 − q n + c ( □ ) ) → 1 (1-q^{n+c(\square)})\to 1 ( 1 − q n + c ( □ ) ) → 1
s λ ( 1 , q , q 2 , … ) = q b ( λ ) ∏ □ ∈ λ 1 ( 1 − q ) [ h λ ( □ ) ] q
s_{\lambda}(1,q,q^2,\ldots)=q^{b(\lambda)}\prod_{\square\in\lambda}\frac{1}{(1-q)[h_{\lambda}(\square)]_q}
s λ ( 1 , q , q 2 , … ) = q b ( λ ) □ ∈ λ ∏ ( 1 − q ) [ h λ ( □ ) ] q 1 となります。2 つの式を合わせることで
∑ T ∈ S Y T ( λ ) q c o m a j ( T ) = q b ( λ ) [ n ] q ! ∏ □ ∈ λ [ h λ ( □ ) ] q
\sum_{T\in\mathrm{SYT}(\lambda)}q^{\mathrm{comaj}(T)}=\frac{q^{b(\lambda)}[n]_q!}{\prod_{\square\in\lambda}[h_{\lambda}(\square)]_q}
T ∈ SYT ( λ ) ∑ q comaj ( T ) = ∏ □ ∈ λ [ h λ ( □ ) ] q q b ( λ ) [ n ] q ! が得られました。最後に maj と comaj の分布が等しいことを示します。これは、標準ヤングタブロー T T T D e s ( T ) = { d 1 , … , d k } \mathrm{Des}(T)=\{d_1,\ldots,d_k\} Des ( T ) = { d 1 , … , d k } D e s ( T ∗ ) = { n − d k , … , n − d 1 } \mathrm{Des}(T^*)=\{n-d_k,\ldots,n-d_1\} Des ( T ∗ ) = { n − d k , … , n − d 1 } T ∗ T^* T ∗
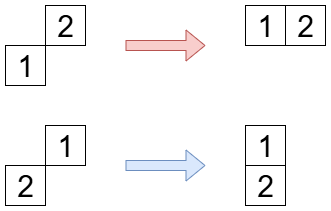
ここで登場するのが、evacuation という全単射です。これは標準ヤングタブロー T T T
T T T i i i n + 1 − i n+1-i n + 1 − i 180°回転する。
スライド操作により標準ヤングタブローにする。
ここでスライド操作とは、次の 2 種類の操作です。英語の文献では jeu de taquin と呼ばれています。
操作によって単調増加性は保たれています。これを繰り返すことで歪ヤングタブローから通常のヤングタブローを得ることができます。得られるタブローはスライド操作を行う順番によらないことが知られています。
evacuation の例を載せます。
1, 2 の操作で降下点集合が { n − d k , … , n − d 1 } \{n-d_k,\ldots,n-d_1\} { n − d k , … , n − d 1 }
よって maj と comaj の分布が等しいことがわかり
∑ T ∈ S Y T ( λ ) q m a j ( T ) = q b ( λ ) [ n ] q ! ∏ □ ∈ λ [ h λ ( □ ) ] q
\sum_{T\in\mathrm{SYT}(\lambda)}q^{\mathrm{maj}(T)}=\frac{q^{b(\lambda)}[n]_q!}{\prod_{\square\in\lambda}[h_{\lambda}(\square)]_q}
T ∈ SYT ( λ ) ∑ q maj ( T ) = ∏ □ ∈ λ [ h λ ( □ ) ] q q b ( λ ) [ n ] q ! が示されました。
q フックウォーク
#
フック長公式の記事ではフックウォークを用いて公式を証明しました。q q q q q q
成瀬のフック長公式の q 類似
#
記念すべき Natori の初回では成瀬のフック長公式を紹介しました。
【月刊組合せ論 Natori】EDPC-T Permutation を深掘り【2022 年 9 月号】
これは歪ヤング図形 λ / μ \lambda/\mu λ / μ
f λ / μ = ∣ n ∣ ! ∑ E ∈ E ∏ □ ∈ λ ∖ E 1 h λ ( □ )
f^{\lambda/\mu}=|n|!\sum_{E\in\mathcal{E}}\prod_{\square\in\lambda\setminus E}\frac{1}{h_{\lambda}(\square)}
f λ / μ = ∣ n ∣ ! E ∈ E ∑ □ ∈ λ ∖ E ∏ h λ ( □ ) 1 ここで n = ∣ λ / μ ∣ n=|\lambda/\mu| n = ∣ λ / μ ∣ E \mathcal{E} E λ / μ \lambda/\mu λ / μ
この式の q q q
s λ / μ = ∑ T ∈ S Y T ( λ / μ ) L D e s ( T )
s_{\lambda/\mu}=\sum_{T\in \mathrm{SYT}(\lambda/\mu)}L_{\mathrm{Des}(T)}
s λ / μ = T ∈ SYT ( λ / μ ) ∑ L Des ( T ) 同様の計算で
s λ / μ ( 1 , q , q 2 , … ) = ∑ T ∈ S Y T ( λ / μ ) q m a j ( T ) ( 1 − q ) ( 1 − q 2 ) ⋯ ( 1 − q n )
s_{\lambda/\mu}(1,q,q^2,\ldots)=\frac{\sum_{T\in\mathrm{SYT}(\lambda/\mu)}q^{\mathrm{maj}(T)}}{(1-q)(1-q^2)\cdots(1-q^n)}
s λ / μ ( 1 , q , q 2 , … ) = ( 1 − q ) ( 1 − q 2 ) ⋯ ( 1 − q n ) ∑ T ∈ SYT ( λ / μ ) q maj ( T ) がわかります。シューア関数については次の式が成り立つことが知られています。
s λ / μ ( 1 , q , q 2 , … ) = ∑ E ∈ E ∏ ( i , j ) ∈ λ ∖ E q λ j ′ − i 1 − q h λ ( i , j )
s_{\lambda/\mu}(1,q,q^2,\ldots)=\sum_{E\in\mathcal{E}}\prod_{(i,j)\in\lambda\setminus E}\frac{q^{\lambda'_j-i}}{1-q^{h_{\lambda}(i,j)}}
s λ / μ ( 1 , q , q 2 , … ) = E ∈ E ∑ ( i , j ) ∈ λ ∖ E ∏ 1 − q h λ ( i , j ) q λ j ′ − i 以上より
∑ T ∈ S Y T ( λ / μ ) q m a j ( T ) = [ n ] q ! ∑ E ∈ E ∏ ( i , j ) ∈ λ ∖ E q λ j ′ − i [ h λ ( i , j ) ] q
\sum_{T\in\mathrm{SYT}(\lambda/\mu)}q^{\mathrm{maj}(T)}=[n]_q!\sum_{E\in\mathcal{E}}\prod_{(i,j)\in\lambda\setminus E}\frac{q^{\lambda_j'-i}}{[h_{\lambda}(i,j)]_q}
T ∈ SYT ( λ / μ ) ∑ q maj ( T ) = [ n ] q ! E ∈ E ∑ ( i , j ) ∈ λ ∖ E ∏ [ h λ ( i , j ) ] q q λ j ′ − i が成り立ちます。
詳しくは Morales, Pak, Panova の論文をご覧ください。
おわりに
#
ヤング図形強化月間ということでヤング図形に関する記事を書きました。過去記事を見返すと、ヤング図形の記事が多いですね。それだけ大好きな概念ということです。
これからも組合せ論の好きな概念を追いかけていきたいので、応援よろしくお願いします。
参考文献
#
Kerov, S. A q-analog of the hook walk algorithm for random Young tableaux. J. Algebr. Comb. 2, No. 4, 383-396 (1993).
Morales, Alejandro H.; Pak, Igor; Panova, Greta. Hook formulas for skew shapes. I: q-analogues and bijections. J. Comb. Theory, Ser. A 154, 350-405 (2018).
Stanley, Richard P. Enumerative combinatorics. Volume 2. Cambridge University Press. (1999).