【月刊組合せ論 Natori】ランダムヤングタブローと北極圏定理【2024 年 9 月号】
目次
月刊組合せ論 Natori は面白そうな組合せ論のトピックを紹介していく企画です。今回は $N\times N$ 型のヤングタブローにおいて $N\to\infty$ としたときにどうなるかを考えていきます。
ヤングタブロー #
$N\times N$ のマス目があります。ここに $1$ から $N^2$ までの整数を 1 つずつ、次の条件を満たすように書き込みます。
- 各行について単調増加
- 各列について単調増加
例えば $N=5$ のときは次のようになります。
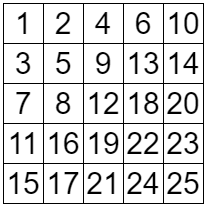
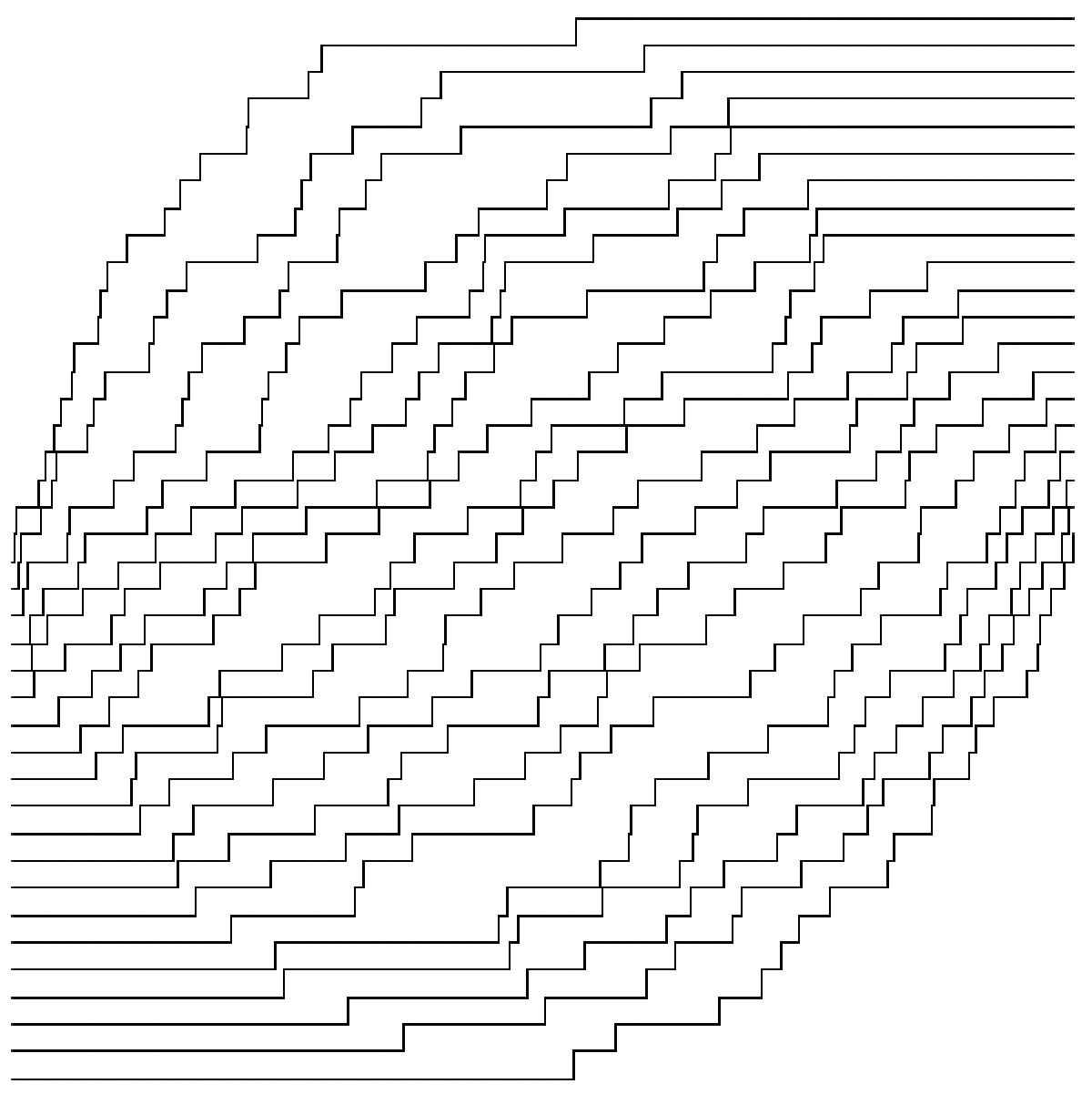
このようなものをヤングタブローといいます。ヤングタブローの中から一様ランダムに 1 つ選んだとき、どのような形になるかを考えます。勿論このままではただの正方形なので、うまく可視化する必要があります。さらに $N\to\infty$ としたときどうなるかを考えます。このようなことを扱う分野を漸近的組合せ論 (asymptotic combinatorics) というそうです。
ヤングタブローの可視化 #
与えられたヤングタブローに対して $N$ 個のグラフを描きます。時刻 0 において $i$ 番目のグラフは高さ $N-i$ にあるものとします。
$k=1,2,\ldots,N^2$ の順に次の操作を行います。
- $k$ がタブローの $i$ 行目にあるとき、時刻 $k$ において $i$ 番目のグラフの高さを 1 増やす。
上のタブローでは次のようなグラフになります。
タブローの単調増加性より、どの 2 本も交わりません。
このグラフは Processing で描画しました。次のようなコードです。
size(500, 500);
background(255);
int[][] a = { { 1,2,4,6,10 },{ 3,5,9,13,14 },{ 7,8,12,18,20 },{ 11,16,19,22,23 },{ 15,17,21,24,25 }};
int n = a.length;
float dx = 480.0 / (n * n);
float dy = 480.0 / (2 * n - 1);
for (int i = 0; i < n; i++) {
float y = 10 + dy * n + dy * i;
float x = 10;
int j = 0;
for (int k = 1; k <= n * n; k++) {
line(x, y, x + dx, y);
x += dx;
if (j < n && a[i][j] == k) {
j++;
line(x, y, x, y - dy);
y -= dy;
}
}
}
それでは $N\to\infty$ としたとき、どのようなグラフになるかを調べていきましょう。
サンプリング #
ここで問題となるのが、ヤングタブローを一様ランダムに選ぶにはどうすればよいかということです。$N$ が大きくなるにつれ、ヤングタブローの個数は膨大になります。
そこで役立つのがフック長公式の証明です。確率を用いた証明ではフックウォークと呼ばれるものが用いられていますが、これが役に立ちます。過去に公開した記事をご覧ください。
【月刊組合せ論 Natori】フック長公式【2023 年 5 月号】
$\lambda$ 上のヤングタブローの個数を $F_{\lambda}$ とします。$\lambda$ から角 $c$ を除いた図形を $\mu$ とするとき、フックウォークの終点が $c$ となる確率が $\frac{F_{\mu}}{F_{\lambda}}$ となることを示していました。このことから、次のようなアルゴリズムによってヤングタブローを一様ランダムに選ぶことができます。
- 箱の総数が $n$ のヤング図形を考える。
- フックウォークを行い、終点に $n$ を書く。
- 残りの図形に再びフックウォークを行い、終点に $n-1$ を書く。
- これを繰り返す。
これを正方形ヤング図形の場合にコードにしたものが次のものになります。(本当はこれも Processing で書きたかったのですが、慣れていないので Kotlin で書きました)
fun main() {
val n = 10
val a = Array(n) { Array(n) { 0 } }
val cells = mutableSetOf<Pair<Int, Int>>()
for (i in 0 until n) {
for (j in 0 until n) {
cells.add(i to j)
}
}
for (num in n * n downTo 1) {
val firstCell = cells.random()
var x = firstCell.first
var y = firstCell.second
while (true) {
val candidates = mutableListOf<Pair<Int, Int>>()
for (i in x + 1 until n) {
if (a[i][y] == 0) {
candidates.add(i to y)
} else {
break
}
}
for (j in y + 1 until n) {
if (a[x][j] == 0) {
candidates.add(x to j)
} else {
break
}
}
if (candidates.isEmpty()) {
break
}
val choice = candidates.random()
x = choice.first
y = choice.second
}
a[x][y] = num
cells.remove(x to y)
}
print("{ ")
print(a.map { "{ ${it.joinToString(",")} }" }.joinToString(","))
println("};")
}
上の Processing のコードの a の定義を、このコードの出力で置き換えればよいです。
いざ実行 #
まずは $N=10$ で実行してみましょう。
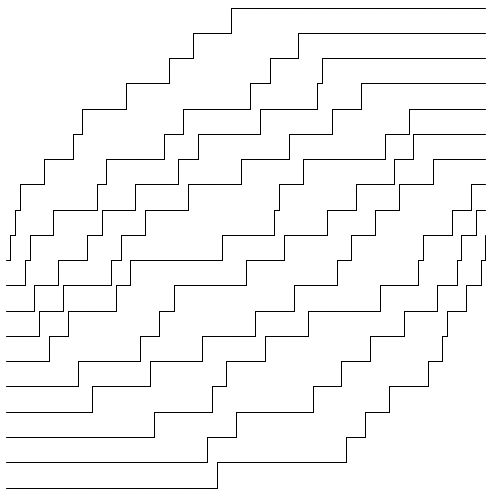
なるほど。
次は $N=20$ で実行してみましょう。
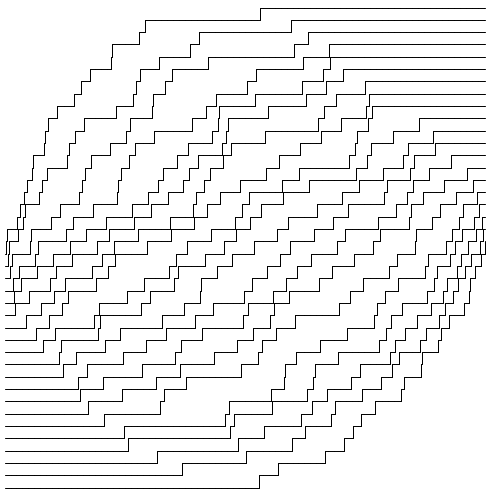
おや？
次は $N=50$ で実行してみましょう。
おやおや？
何やら円が見えますね。円の内側で動いており、外側ではほとんど動かないようです。これが $N\to\infty$ としたときに見えてくる形です。このような現象は六角形のひし形タイル張りや、アステカダイヤモンドのドミノタイル張りなどでも現れ、arctic circle theorem と呼ばれています。直訳すると北極圏定理でしょうか。
おわりに #
組合せ論と確率論の関係というと、高校数学では当たり前という感じがしますが、大学数学では非自明で、奥深く、豊かな関係があります。この辺りももっと知りたいです。
参考文献 #
- Romik, Dan. Arctic circles, domino tilings and square Young tableaux. Ann. Probab. 40, No. 2, 611-647 (2012).
- Romik, Dan. The surprising mathematics of longest increasing subsequences. Cambridge University Press. (2015).