↓メインコンテンツへスキップ
組合せ論、楽しい！

【月刊組合せ論 Natori】フック長公式【2023 年 5 月号】

·
箱星
著者
箱星
のんびり暮らしたい。
目次

月刊組合せ論 Natori は面白そうな組合せ論のトピックを紹介していく企画です。今回はヤング図形好きなら外せない、フック長公式について深掘りしていきます。

フック長公式
#

フック長公式は標準タブローの個数を数える公式です。標準タブローはヤング図形のマスに 1 から nn までの正の整数を一回ずつ書き込んだもので、各行・各列について単調増加なものです。

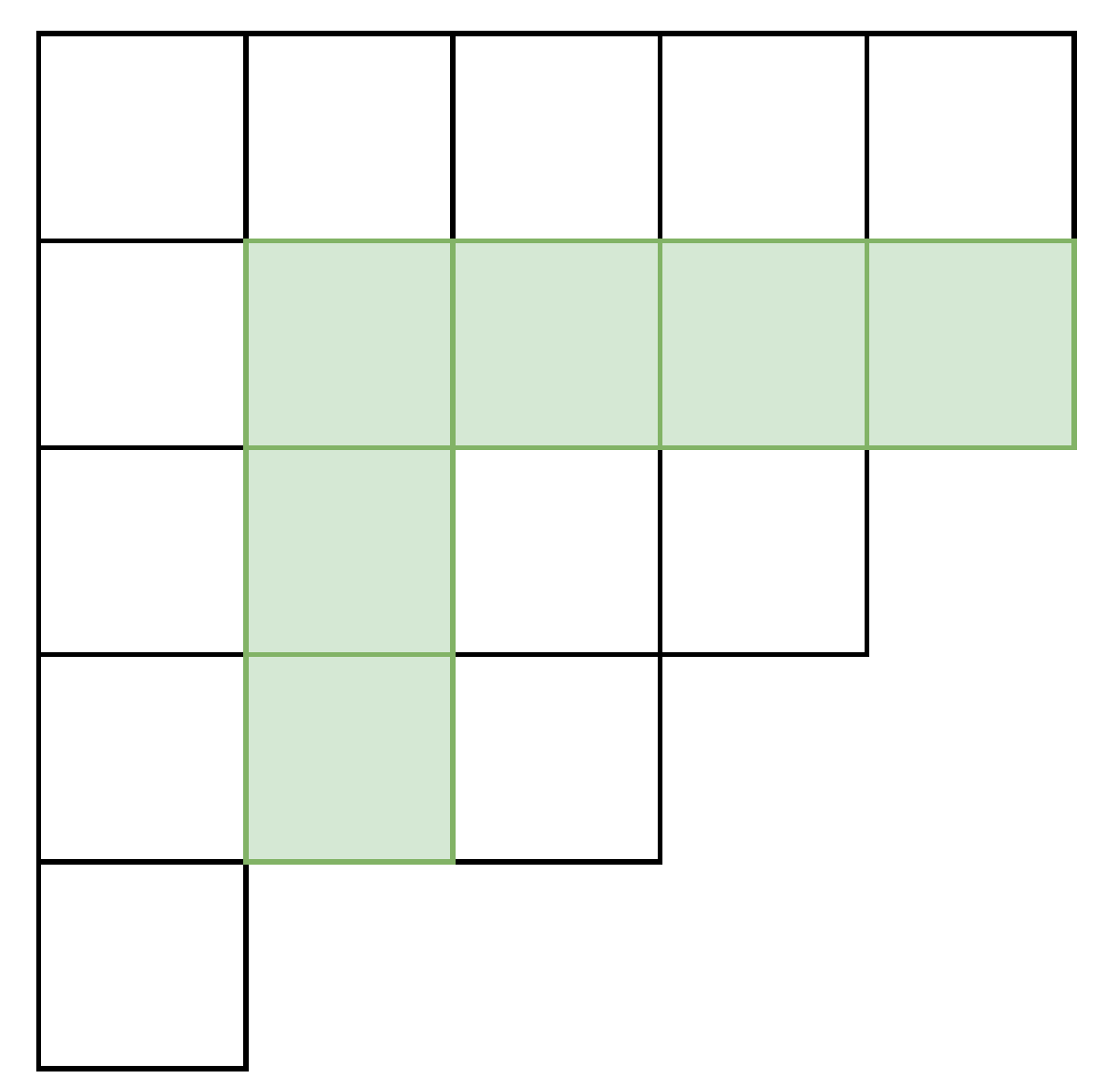
フックとは、あるマスとその右・下にあるマスからなる集合です。

フック長公式によると、標準タブローの個数は

n!∏(i,j)∈λh(i,j) \frac{n!}{\prod_{(i,j)\in\lambda} h(i,j)}

により求められます。ここで h(i,j)h(i,j) はフック長、すなわちフックに含まれるマスの個数です。λ\lambda を明示して hλ(i,j)h_{\lambda}(i,j) と書くこともあります。すべてのマスについてフック長を計算し、その総積で n!n! を割った値が標準タブローの個数ということです。

以下ではフック長公式の証明をいくつか紹介します。1 つ目の証明のみ詳述し、残りは概略を述べるだけとします。

確率論的証明
#

この証明が恐らくもっとも有名ではないでしょうか。

λ\lambda 上の標準タブローの個数を DλD_{\lambda} とおき、Fλ=n!∏(i,j)∈λh(i,j)F_{\lambda}=\frac{n!}{\prod_{(i,j)\in\lambda}h(i,j)} とおきます。

λ\lambda の隅とは、右にも下にもマスがないようなマスをいいます。最大の数 nn が書き込まれるのは隅です。この隅を削除するとサイズ n−1n-1 の標準タブローが得られます。よって DλD_{\lambda} は次の漸化式を満たします。

Dλ=∑μ↗λDμ D_{\lambda}=\sum_{\mu\nearrow\lambda}D_{\mu}

ここで μ↗λ\mu\nearrow\lambda は λ\lambda から隅を 1 個削除することで μ\mu が得られることを表しています。このような μ\mu 全体について和をとるという意味です。

λ=(1)\lambda=(1) のとき Dλ=Fλ=1D_{\lambda}=F_{\lambda}=1 なので、FλF_{\lambda} が同じ漸化式

Fλ=∑μ↗λFμ F_{\lambda}=\sum_{\mu\nearrow\lambda}F_{\mu}

をみたすことを示せばよいです。この式を ∑FμFλ=1\sum\frac{F_{\mu}}{F_{\lambda}}=1 と書き換えます。この式を確率的に解釈していきましょう。

ヤング図形 λ\lambda 上のフックウォークを定義します。

  • まず λ\lambda のマスを一様ランダムに 1 つ選び、(x1,y1)(x_1,y_1) とします。
  • 次に (x1,y1)(x_1,y_1) に関するフックから (x1,y1)(x_1,y_1) を除いた集合が空でないとき、その中から一様ランダムにマスを 1 つ選び、(x2,y2)(x_2,y_2) とします。
  • これを繰り返します。

選んだマスを並べた (x1,y1),(x2,y2),…,(xk,yk)(x_1,y_1),(x_2,y_2),\ldots, (x_k,y_k) をフックウォークと呼びます。フックウォークの終点 (xk,yk)(x_k,y_k) は隅となります。このとき次の命題が成り立ちます。

命題: 隅 (a,b)(a,b) に対して、フックウォークの終点が (a,b)(a,b) となる確率は FμFλ\frac{F_{\mu}}{F_{\lambda}} である。ここで μ\mu は λ\lambda から (a,b)(a,b) を除いた図形である。

必ず終点が隅になることから確率の総和は 1 なので、この命題から示すべき式が従います。

命題を証明します。(i,j)(i,j) が隅 (a,b)(a,b) と同じ行にも列にもないとき hλ(i,j)=hμ(i,j)h_{\lambda}(i,j)=h_{\mu}(i,j) であることに注意すると

FμFλ=(n−1)!/∏(i,j)∈μhμ(i,j)n!/∏(i,j)∈λhλ(i,j)=1n∏(i,j)∈λhλ(i,j)∏(i,j)∈μhμ(i,j)=1n∏i=1a−1hλ(i,b)hλ(i,b)−1∏j=1b−1hλ(a,j)hλ(a,j)−1=1n∏i=1a−1(1+1hλ(i,b)−1)∏j=1b−1(1+1hλ(a,j)−1) \begin{align*} \frac{F_{\mu}}{F_{\lambda}} &= \frac{(n-1)!/\prod_{(i,j)\in \mu}h_{\mu}(i,j)}{n!/\prod_{(i,j)\in \lambda}h_{\lambda}(i,j)} \\ &= \frac{1}{n}\frac{\prod_{(i,j)\in\lambda}h_{\lambda}(i,j)}{\prod_{(i,j)\in\mu}h_{\mu}(i,j)} \\ &= \frac{1}{n}\prod_{i=1}^{a-1}\frac{h_{\lambda}(i,b)}{h_{\lambda}(i,b)-1}\prod_{j=1}^{b-1}\frac{h_{\lambda}(a,j)}{h_{\lambda}(a,j)-1} \\ &= \frac{1}{n}\prod_{i=1}^{a-1}\left(1+\frac{1}{h_{\lambda}(i,b)-1}\right)\prod_{j=1}^{b-1}\left(1+\frac{1}{h_{\lambda}(a,j)-1}\right) \end{align*}

となります。展開すると

FμFλ=1n∑A⊆{1,…,a−1}∑B⊆{1,…,b−1}Q(A,B)Q(A,B)=∏i∈A1hλ(i,b)−1∏j∈B1hλ(a,j)−1 \begin{gather*} \frac{F_{\mu}}{F_{\lambda}}=\frac{1}{n}\sum_{A\subseteq\{1,\ldots,a-1\}}\sum_{B\subseteq\{1,\ldots,b-1\}}Q(A,B) \\ Q(A,B)=\prod_{i\in A}\frac{1}{h_{\lambda}(i,b)-1}\prod_{j\in B}\frac{1}{h_{\lambda}(a,j)-1} \end{gather*}

となります。

ここで部分集合 A,BA,B に対して、フックウォークの始点が (min⁡(A∪{a}),min⁡(B∪{b}))(\min(A\cup\{a\}), \min(B\cup\{b\}))、終点が (a,b)(a,b) になるという条件の下で、フックウォークの行番号の集合が A∪{a}A\cup\{a\}、列番号の集合が B∪{b}B\cup\{b\} になる条件付き確率を P(A,B)P(A,B) とします。P(A,B)=Q(A,B)P(A,B)=Q(A,B) を示せば命題が示されます。

∣A∣+∣B∣|A|+|B| に関する帰納法を用います。AA または BB が空集合のときは簡単にわかるので、そうでないとします。x1=min⁡A,y1=min⁡Bx_1=\min A, y_1=\min B とおきます。P(A,B)=1hλ(x1,y1)−1(P(A∖{x1},B)+P(A,B∖{y1}))P(A,B)=\frac{1}{h_{\lambda}(x_1,y_1)-1}(P(A\setminus\{x_1\}, B)+P(A,B\setminus\{y_1\})) です。帰納法の仮定より

P(A∖{x1},B)=Q(A∖{x1},B)=∏i∈A∖{x1}1hλ(i,b)−1∏j∈B1hλ(a,j)−1=(hλ(x1,b)−1)Q(A,B) \begin{align*} P(A\setminus\{x_1\}, B) &= Q(A\setminus\{x_1\}, B) \\ &= \prod_{i\in A\setminus\{x_1\}}\frac{1}{h_{\lambda}(i,b)-1}\prod_{j\in B}\frac{1}{h_{\lambda}(a,j)-1} \\ &= (h_{\lambda}(x_1,b)-1)Q(A,B) \end{align*}

同様に

P(A,B∖{y1})=(hλ(a,y1)−1)Q(A,B) P(A,B\setminus\{y_1\})=(h_{\lambda}(a,y_1)-1)Q(A,B)

となるので

P(A,B)=hλ(x1,b)−1+hλ(a,y1)−1hλ(x1,y1)−1Q(A,B)=Q(A,B) P(A,B)=\frac{h_{\lambda}(x_1,b)-1+h_{\lambda}(a,y_1)-1}{h_{\lambda}(x_1,y_1)-1}Q(A,B)=Q(A,B)

となります。

全単射
#

全単射を用いた証明がいくつかあります。FλF_{\lambda} を標準タブローの個数とします。分母を払って n!=Fλ∏(i,j)h(i,j)n!=F_{\lambda}\prod_{(i,j)}h(i,j) を示せばよいです。ここで a(i,j)a(i,j) を (i,j)(i,j) より右にあるマスの個数、l(i,j)l(i,j) を (i,j)(i,j) より下にあるマスの個数とすると、h(i,j)=a(i,j)+l(i,j)+1h(i,j)=a(i,j)+l(i,j)+1 となります。ゆえに −l(i,j)-l(i,j) 以上 a(i,j)a(i,j) 以下の整数の個数は h(i,j)h(i,j) です。マス (i,j)(i,j) に書かれている数が −l(i,j)-l(i,j) 以上 a(i,j)a(i,j) 以下であるようなタブローをフックタブローと呼ぶことにします。

標準タブローの個数が FλF_{\lambda}、フックタブローの個数が ∏(i,j)h(i,j)\prod_{(i,j)}h(i,j) であることから、標準タブローとフックタブローの組が順列と一対一対応することを示せばよいです。

詳しくは Sagan の教科書で解説されています。

表現論
#

ヤング図形は対称群の表現論と深くかかわります。例えば対称群 SnS_n の既約表現はサイズ nn のヤング図形と一対一に対応し、λ\lambda に対応する既約表現の次元は λ\lambda 上の標準タブローの個数と等しくなります。

フロベニウスの指標公式と呼ばれるものがあり、そこから証明することができるようです。『テンソル代数と表現論』を参照してください。

複素解析
#

複素解析を用いた証明もあります。以下の文献で解説されています。

ヤング図形の組合せ論講義

幾何学
#

幾何学な証明は

  • Pak, Igor. Hook length formula and geometric combinatorics. Sémin. Lothar. Comb. 46, B46f, 13 p. (2001).

にあるようです。(読んでいないのでわかりません……)

おわりに
#

今回はフック長公式の様々な証明を紹介しました。1 つの公式にいろいろな証明があるのは面白いですね。

今後も月刊組合せ論 Natori では様々なトピックを紹介予定なので、応援のほどよろしくお願いいたします。

参考文献
#

  • 池田岳. テンソル代数と表現論. 東京大学出版会. (2022).
  • Romik, Dan. The surprising mathematics of longest increasing subsequences. Cambridge University Press. (2015).
  • Sagan, Bruce E. The symmetric group. Representations, combinatorial algorithms, and symmetric functions. 2nd ed. Springer. (2001).