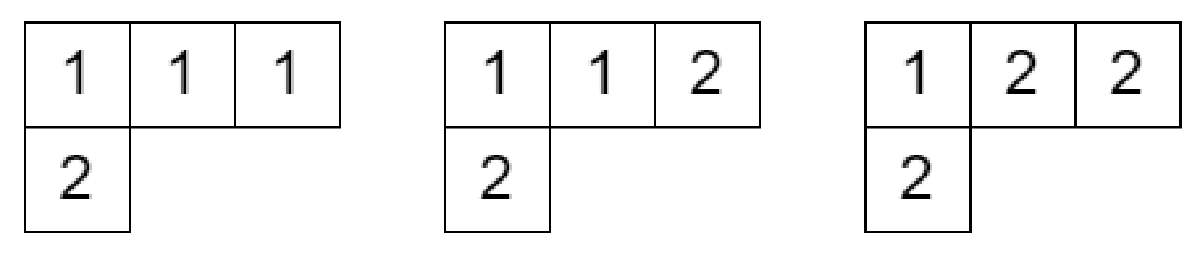↓メインコンテンツへスキップ
組合せ論、楽しい！

【月刊組合せ論 Natori】シューア多項式とヤコビ・トゥルーディ公式【2023 年 3 月号】

·
箱星
著者
箱星
のんびり暮らしたい。
目次

月刊組合せ論 Natori は面白そうな組合せ論のトピックを紹介していく企画です。今回は組合せ論・対称関数論を中心に幅広く活躍するシューア多項式について語っていきます。

半標準タブロー
#

ヤング図形のマスに正整数を書き込んだものであって

  • 各行について広義単調増加
  • 各列について狭義単調増加

となるものを半標準タブローといいます。

シューア多項式
#

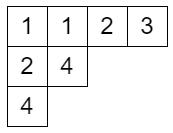
ヤング図形 λ\lambda 上の半標準タブローのうち、書き込まれた整数が nn 以下であるもの全体からなる集合を SST(λ,n)\text{SST}(\lambda,n) とします。

SST((3,1),1)\text{SST}((3,1),1) は空集合で、SST((3,1),2)\text{SST}((3,1),2) は次の 33 つのタブローからなる集合です。

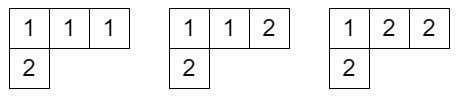
ここで x1,x2x_1,x_2 という記号 (不定元) を導入して、タブローごとに 11 の個数だけ x1x_1 をかけ、22 の個数だけ x2x_2 をかけた単項式を作ります。上の例ではそれぞれ x13x2,x12x22,x1x23x_1^3x_2, x_1^2x_2^2, x_1x_2^3 となります。これらの和を

s(3,1)(x1,x2)=x13x2+x12x22+x1x23 s_{(3,1)}(x_1,x_2)=x_1^3x_2+x_1^2x_2^2+x_1x_2^3

とします。このようにしてできる多項式をシューア多項式といいます。

一般にシューア多項式 sλ(x1,x2,…,xn)s_{\lambda}(x_1,x_2,\ldots,x_n) は次のように定義されます。T∈SST(λ,n)T\in\text{SST}(\lambda,n) に対して、TT に書き込まれた整数 ii の個数を cic_i とするとき

sλ(x1,x2,…,xn)=∑T∈SST(λ,n)x1c1⋯xncn s_{\lambda}(x_1,x_2,\ldots,x_n)=\sum_{T\in \text{SST}(\lambda,n)}x_1^{c_1}\cdots x_n^{c_n}

と定義します。ぜひ手ごろな例で計算してみましょう。

いくつか計算してみると、sλs_{\lambda} が対称多項式となっていることに気づくと思います。定義からは非自明ですね。組合せ論的には Bender-Knuth involution というものを使えば証明できるらしいですが、今回は別の方法で証明しましょう。

代数的定義
#

次の 2 つの行列式を考えます。

Δ1=det⁡(x14x24x1x2)Δ2=det⁡(x1x211) \begin{align*} \Delta_1&=\det\begin{pmatrix} x_1^4 & x_2^4 \\ x_1 & x_2 \end{pmatrix} \\ \Delta_2&=\det\begin{pmatrix} x_1 & x_2 \\ 1 & 1 \end{pmatrix} \end{align*}

計算すると

Δ1=x14x2−x1x24=x1x2(x1−x2)(x12+x1x2+x22)Δ2=x1−x2 \begin{align*} \Delta_1 &= x_1^4x_2-x_1x_2^4=x_1x_2(x_1-x_2)(x_1^2+x_1x_2+x_2^2) \\ \Delta_2 &= x_1-x_2 \end{align*}

となります。Δ1\Delta_1 は Δ2\Delta_2 で割り切れるので比を計算すると、Δ1/Δ2=x13x2+x12x22+x1x23\Delta_1/\Delta_2=x_1^3x_2+x_1^2x_2^2+x_1x_2^3 となります。これは上で計算した s(3,1)(x1,x2)s_{(3,1)}(x_1,x_2) と等しいです。

このように、シューア多項式は 2 つの行列式の比として定義することも可能です。α=(a1,a2,…,an)\alpha=(a_1,a_2,\ldots,a_n) に対して Aα(x1,x2,…,xn)=det⁡(xiaj)A_{\alpha}(x_1,x_2,\ldots,x_n)=\det(x_i^{a_j}) とおきます。δn=(n−1,n−2,…,1,0)\delta_n=(n-1,n-2,\ldots,1,0) とおき、λ+δn=(λ1+n−1,λ2+n−2,…,λn−1+1,λn)\lambda+\delta_n=(\lambda_1+n-1,\lambda_2+n-2,\ldots,\lambda_{n-1}+1,\lambda_n) とするとき

Aλ+δn(x1,x2,…,xn)Aδn(x1,x2,…,xn) \frac{A_{\lambda+\delta_n}(x_1,x_2,\ldots,x_n)}{A_{\delta_n}(x_1,x_2,\ldots,x_n)}

をシューア多項式の定義とすることもあります。2 つの定義が同値であることがわかれば、2 つの世界を行き来することで様々な性質がわかります。例えば、行列式の性質から xix_i と xjx_j を入れ替えると Aα(x1,x2,…,xn)A_{\alpha}(x_1,x_2,\ldots,x_n) は −1-1 倍となるので、シューア多項式は分母分子で打ち消しあって不変となります。こちらの定義では対称多項式であることが簡単に示せます。

ヤコビ・トゥルーディ公式
#

定義の同値性を示す鍵となるのが次のヤコビ・トゥルーディ公式です。

sλ(x1,…,xn)=det⁡(hλi−i+j(x1,…,xn)) s_{\lambda}(x_1,\ldots,x_n)=\det(h_{\lambda_i-i+j}(x_1,\ldots,x_n))

ここで hk(x1,…,xn)h_k(x_1,\ldots,x_n) は完全対称多項式で、次のように定義されます。

hk(x1,…,xn)=∑1≤i1≤i2≤⋯≤ik≤nxi1xi2⋯xik h_k(x_1,\ldots,x_n)=\sum_{1\le i_1\le i_2\le\cdots\le i_k\le n}x_{i_1}x_{i_2}\cdots x_{i_k}

ヤコビ・トゥルーディ公式の証明には LGV 公式を用います。LGV 公式については 2022 年 9 月号をご覧ください。

定理 (LGV): 条件「i1<i2,j1>j2i_1<i_2, j_1>j_2 ならば ai1a_{i_1} から bj1b_{j_1} へのパスと ai2a_{i_2} から bj2b_{j_2} へのパスは必ず交わる」を仮定する。このとき

det⁡M(a,b)=∑(P1,…,Pn)w(P1)⋯w(Pn) \det M(a,b)=\sum_{(P_1,\ldots,P_n)}w(P_1)\cdots w(P_n)

が成り立つ。ここで和は PiP_i が aia_i から bib_i へのパスでどの 2 つも互いに交わらないもの全体をわたる。

グラフを次のように構成します。V={(i,j)∈Z2∣1≤i≤(十分大きな値),1≤j≤n}V=\{(i,j)\in\mathbb{Z}^2\mid 1\le i\le \text{(十分大きな値)}, 1\le j\le n\} とし、(i,j)(i,j) から (i+1,j)(i+1,j) に重み xjx_j の辺を張り、(i,j)(i,j) から (i,j+1)(i,j+1) に重み 1 の辺を張ります。

このとき、∑P:(i,1)→(i+k,n)w(P)=hk(x)\sum_{P:(i,1)\to (i+k,n)}w(P)=h_k(x) となります。

ai=(n+1−i,1),bi=(λi+n+1−i,n) (i=1,…,n)a_i=(n+1-i,1), b_i=(\lambda_i+n+1-i, n) \ (i=1,\ldots,n) とおくと、LGV 公式の左辺は det⁡(hλj−j+i)=det⁡(hλi−i+j)\det(h_{\lambda_j-j+i})=\det(h_{\lambda_i-i+j}) になります。

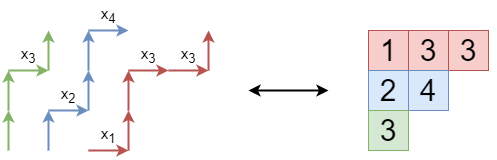
パス Pi ⁣:ai→biP_i\colon a_i\to b_i について w(Pi)=xj1⋯xjk (j1≤j2≤⋯≤jk)w(P_i)=x_{j_1}\cdots x_{j_k} \ (j_1\le j_2\le \cdots\le j_k) のとき、ii 行目の数字を j1,…,jkj_1,\ldots,j_k としたタブローを作ります。パスが互いに交わらないことはタブローの列の狭義増加性に対応します。よってこれは半標準タブローです。逆に半標準タブローから互いに交わらないパスの組を復元できるので、LGV 公式の右辺は ∑T∈SST(λ,n)x1c1⋯xncn=sλ(x)\sum_{T\in \mathrm{SST}(\lambda,n)}x_1^{c_1}\cdots x_n^{c_n}=s_{\lambda}(x) となります。

これでヤコビ・トゥルーディ公式が示されました。

同値性の証明
#

ai′=(n+1−i,i)a_i^{\prime}=(n+1-i,i) とおくと、互いに交わらないパス Pi ⁣:ai→biP_i\colon a_i\to b_i において aia_i から ai′a_i^{\prime} までまっすぐ上に進むことがわかります。よって始点を ai′a_i^{\prime} に変更しても影響なく、上の結果から det⁡M(a′,b)=sλ(x)\det M(a^{\prime},b)=s_{\lambda}(x) となります。

(i,j)(i,j) から (i+1,j)(i+1,j) への辺の重みを xj−xi+jx_j-x_{i+j} に変更します。ただし xn+1=xn+2=⋯=0x_{n+1}=x_{n+2}=\cdots=0 とします。ai′a_i^{\prime} から bib_i へのパスにおいて影響はないので、引き続き det⁡M(a′,b)=sλ(x)\det M(a^{\prime},b)=s_{\lambda}(x) です。

ai′′=(1,i)a_i^{\prime\prime}=(1,i) とします。このとき M(a′′,b)=M(a′′,a′)M(a′,b)M(a^{\prime\prime},b)=M(a^{\prime\prime},a^{\prime})M(a^{\prime},b) が成り立ちます。det⁡M(a′′,a′)=∏i<j(xi−xj)=Aδn(x)\det M(a^{\prime\prime},a^{\prime})=\prod_{i<j}(x_i-x_j)=A_{\delta_n}(x) となります。det⁡M(a′′,b)\det M(a^{\prime\prime},b) を計算するために次の補題を用います。

∑P:(1,t)→(m,n)w(P)=(xt−xn+1)(xt−xn+2)⋯(xt−xm+n−1) \sum_{P:(1,t)\to (m,n)}w(P)=(x_t-x_{n+1})(x_t-x_{n+2})\cdots (x_t-x_{m+n-1})

これは m+nm+n に関する帰納法でわかります。これより det⁡M(a′′,b)=det⁡(xiλj+n−j)=Aλ+δn(x)\det M(a^{\prime\prime},b)=\det(x_i^{\lambda_j+n-j})=A_{\lambda+\delta_n}(x) となります。よって sλ(x)=Aλ+δn(x)/Aδn(x)s_{\lambda}(x)=A_{\lambda+\delta_n}(x)/A_{\delta_n}(x) が得られ、シューア多項式の 2 つの定義が同値であることがわかりました。

おわりに
#

シューア多項式の基本的な部分を解説しました。まだまだ面白い話題がいっぱいあるので、今後の号でも取り上げる予定です。

参考文献
#

  • Prasad, Amritanshu. An introduction to Schur polynomials. Grad. J. Math. 4, No. 2, 62-84 (2019).
  • Xiong, Rui. Schur Polynomials through Lindström Gessel Viennot Lemma. arXiv. https://arxiv.org/abs/2003.09215