【月刊組合せ論 Natori】ヤング図形のコア【2023 年 1 月号】

月刊組合せ論 Natori は面白そうな組合せ論のトピックを紹介していく企画です。あけましておめでとうございます。本年も月刊組合せ論 Natori をよろしくお願いいたします。新年一発目となる今回はヤング図形を扱っていきます。

yukicoder

#

yukicoder の Advent Calendar Contest 2022 にて次の問題を出題しました。

No.2149 Vanitas Vanitatum

広義単調増加な正整数列 $(A_1,A_2,\ldots,A_N)$ が与えられます。以下の $2$ 種類の操作を考えます。

• $A_i\ge 2$ となる添字 $i$ を $1$ つ選び、$A_i$ から $2$ を引く。操作後も数列は広義単調増加でなければならない。
• $A_i=A_{i+1}\ge 1$ となる添字 $i$ を $1$ つ選び、$A_i,A_{i+1}$ から $1$ を引く。操作後も数列は広義単調増加でなければならない。

どちらの操作も行えなくなるまで操作を繰り返します。$A_1,A_2,\ldots,A_N$ をすべて $0$ にする操作方法の数を $998244353$ で割った余りを求めてください。

例えば与えられた数列が $(3,3)$ の場合

• $(3,3) \to (2,2) \to (1,1) \to (0,0)$
• $(3,3) \to (2,2) \to (0,2) \to (0,0)$
• $(3,3) \to (1,3) \to (1,1) \to (0,0)$

の 3 通りがあります。

以下ではこの問題の数学的な背景を解説していきます。

論文

#

この問題は論文を読んで得た知識を競プロ用に加工したものです。 [1] の式 (8) にこの問題の答えとなる式が書かれています。

詳しいことはよくわかっていませんが、代数幾何・数論・表現論・数理物理など様々な分野とかかわる論文です。

マヤ図形

#

広義単調増加な正整数列を反転して分割（すなわち広義単調減少な正整数列）にしておきます。そしてヤング図形に変換します。

与えられたヤング図形の境界線に注目して経路を得ます。直線状に並んだマス目の上に、上に進む部分と対応する場所に黒石を置いた図形を考えます。この図形をマヤ図形といいます。

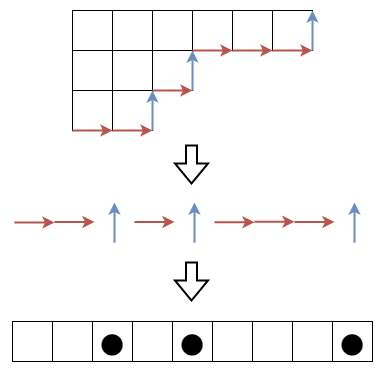
次のように厳密に定義することも可能です。$\lambda=(\lambda_1,\ldots,\lambda_l)$ を分割とします。$\lambda_{l+1}=\lambda_{l+2}=\cdots=0$ としておきます。このとき、数直線上の座標 $\lambda_i-i$ に黒石を置いて得られる図形をマヤ図形といいます。上の図では $\lambda=(6,3,2)$ なので、座標 $5,1,-1,-4,-5,-6,\ldots$ に黒石が置かれます。十分左側ではすべてが黒石になり、十分右側ではすべてが空白となります。

t-quotient

#

問題文の 2 つの操作は、ヤング図形の言葉では縦向き又は横向きのドミノを抜く操作と対応します。マヤ図形では黒石を 2 つ左の空きスペースに動かすという操作に対応します。1 つ左が黒石か空きスペースかどうかで操作が 2 通りにわかれます。

いま、マヤ図形を座標が偶数の部分と奇数の部分にわけます。すると操作は黒石を 1 つ左の空きスペースに動かすことに対応します。ヤング図形の言葉ではマスを 1 つ削除する操作と対応します。扱いやすくなった気がしますね。

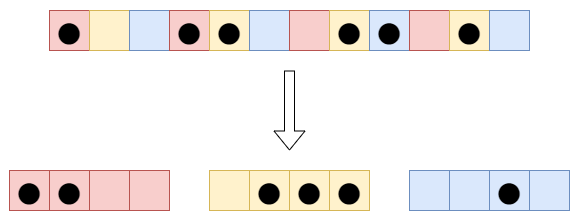
一般に $t$ を 2 以上の整数とし、各 $i=0,1,\ldots,t-1$ に対して、$\bmod{t}$ で $i$ と合同な数を座標にもつマスを取り出すことで $t$ 個のマヤ図形からなる組が得られます。これを $t$-quotient といいます。

$t=3$ の場合は次の図のようになります。

t-core

#

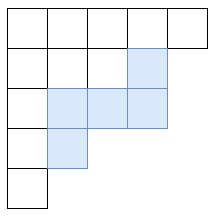
ヤング図形でドミノを取り去る操作は、2-quotient を構成するマヤ図形の 1 つにおいて黒石を 1 つ左に動かす操作となります。

これを一般化すると、$t$-quotient を構成するマヤ図形の 1 つにおいて黒石を 1 つ左に動かす操作は、ヤング図形でサイズ $t$ のリムフックと呼ばれる図形を取り去る操作になります。

さて、ドミノを抜くことを一般化すると、サイズ $t$ のリムフックを抜いていくことになります。

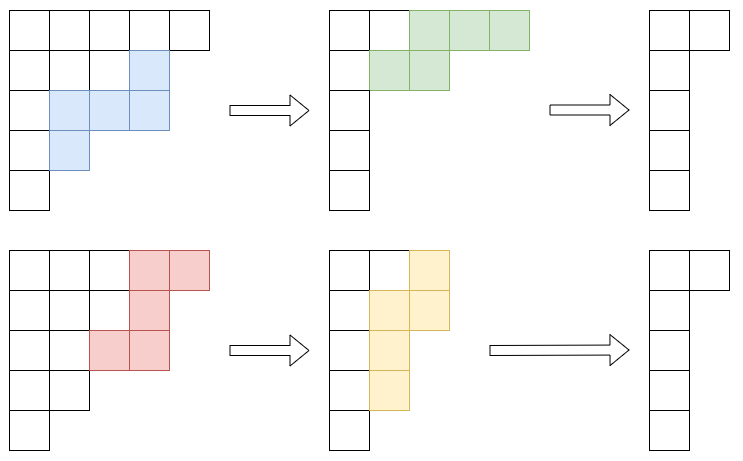
操作を繰り返すと、これ以上リムフックを抜けないような図形になります。どのような順番で抜いても最後の図形は同じになることが示せます。この図形を $t$-core といいます。

2-core は $\emptyset, (1), (2,1), (3,2,1),\ldots$ になります。階段状の図形です。

フック長公式

#

ここまでの流れをまとめると

• 広義単調増加な正整数列をヤング図形に変換する
• さらにマヤ図形に変換する
• マヤ図形の 2-quotient を考える
• 2-quotient を構成する 2 つのマヤ図形から 2 つのヤング図形を得る

おおむね次の問題が解ければよいことになります。

ヤング図形であるという性質を保ったまま 1 つずつマスを削除していく方法は何通りありますか。

これは 2022 年 9 月号でも少し触れたフック長公式を使うことで解くことができます。

ただし 2-core が空でない場合、答えは 0 通りであることに注意が必要です。

対称群の指標表との関係

#

発展的な話として、この問題が対称群の表現論とも関係することに触れていきたいと思います。

$n$ 次対称群の指標表の値は 2 つの $n$ の分割 $\lambda,\mu$ を用いて $\chi_{\lambda}(C_{\mu})$ のように表されます。ここで $\mu=(2,2,\ldots,2)$ としたときの $\chi_{\lambda}(C_{\mu})$ の絶対値が今回の問題の答えと等しくなります。

対称群の指標表の値を求める方法としてムルナガン・中山の規則があり、これを用いて証明することができます。

$\mu=(t,t,\ldots,t)$ の場合に一般化することもできます。

おわりに

#

数学で勉強したことを競プロの問題として出題できて楽しかったです。またこのように知識をお届けしたいです。

今年も月刊組合せ論 Natori を頑張って書いていきたいと思っているので、応援のほどよろしくお願いいたします。

参考文献

#

1. Eskin, Alex; Okounkov, Andrei. Pillowcases and quasimodular forms. Algebraic geometry and number theory. In Honor of Vladimir Drinfeld’s 50th birthday. Progress in Mathematics 253, 1-25 (2006).
2. James, Gordon; Kerber, Adalbert. The representation theory of the symmetric group. Cambridge University Press (2009).
3. Stanley, Richard P. Enumerative combinatorics. Volume 2. Cambridge University Press. (1999).
4. 【大学数学】学校で習わない「自由な割り算」 - 箱の並びを割る, https://zenn.dev/339/articles/9ca3b883a85508