月刊組合せ論 Natori は面白そうな組合せ論のトピックを紹介していく企画です。Natori の名前の由来は combinatorics の natori の部分です。月刊とついていますが毎月更新できないこともあると思われます (ゆるして)。
創刊号の今回はなんと無料!(ずっと無料です)
EDPC-T Permutation
#
今回は EDPC-T Permutation という問題を紹介します。これは競技プログラミングの問題で、与えられた入力に対して適切な出力を行うプログラムを書くことが求められます。問題内容はリンク先をご覧ください。
実はこの問題は数学的に奥が深く、様々な研究がされてきました。その歴史も古く、1908 年の MacMahon の論文にも登場します。
この記事ではこの問題を数学的に深掘りすることを目標にします。
descent set
#
( 1 , 2 , … , n ) (1,2,\ldots,n) ( 1 , 2 , … , n ) ( p 1 , p 2 , … , p n ) (p_1,p_2,\ldots,p_n) ( p 1 , p 2 , … , p n ) descent set を
{ 1 ≤ i < n ∣ p i > p i + 1 }
\{1\le i\lt n\mid p_i>p_{i+1}\}
{ 1 ≤ i < n ∣ p i > p i + 1 } により定めます。例えば ( 3 , 1 , 2 , 5 , 4 ) (3,1,2,5,4) ( 3 , 1 , 2 , 5 , 4 ) { 1 , 4 } \{1,4\} { 1 , 4 }
descent set を用いることで、今考えている問題は次のように言い換えられます。
{ 1 , 2 , … , n − 1 } \{1,2,\ldots,n-1\} { 1 , 2 , … , n − 1 } S S S S S S
包除原理
#
例として n = 6 n=6 n = 6 { 3 } \{3\} { 3 } p 1 < p 2 < p 3 > p 4 < p 5 < p 6 p_1<p_2<p_3>p_4<p_5<p_6 p 1 < p 2 < p 3 > p 4 < p 5 < p 6
まず p 1 < p 2 < p 3 ? p 4 < p 5 < p 6 p_1<p_2<p_3 \ ? \ p_4<p_5<p_6 p 1 < p 2 < p 3 ? p 4 < p 5 < p 6 p 3 , p 4 p_3,p_4 p 3 , p 4 p 1 , p 2 , p 3 p_1,p_2,p_3 p 1 , p 2 , p 3 ( 6 3 ) = 20 \binom{6}{3}=20 ( 3 6 ) = 20 p 4 , p 5 , p 6 p_4,p_5,p_6 p 4 , p 5 , p 6 p 1 < p 2 < p 3 < p 4 < p 5 < p 6 p_1<p_2<p_3<p_4<p_5<p_6 p 1 < p 2 < p 3 < p 4 < p 5 < p 6 p 1 < p 2 < p 3 > p 4 < p 5 < p 6 p_1<p_2<p_3>p_4<p_5<p_6 p 1 < p 2 < p 3 > p 4 < p 5 < p 6 20 − 1 = 19 20-1=19 20 − 1 = 19
同様に descent set が { 3 , 5 } \{3,5\} { 3 , 5 }
p 1 < p 2 < p 3 < p 4 < p 5 < p 6 p_1<p_2<p_3<p_4<p_5<p_6 p 1 < p 2 < p 3 < p 4 < p 5 < p 6 1 1 1 p 1 < p 2 < p 3 ? p 4 < p 5 < p 6 p_1<p_2<p_3 \ ? \ p_4<p_5<p_6 p 1 < p 2 < p 3 ? p 4 < p 5 < p 6 ( 6 3 ) = 20 \binom{6}{3}=20 ( 3 6 ) = 20 p 1 < p 2 < p 3 < p 4 < p 5 ? p 6 p_1<p_2<p_3<p_4<p_5 \ ? \ p_6 p 1 < p 2 < p 3 < p 4 < p 5 ? p 6 ( 6 5 ) = 6 \binom{6}{5}=6 ( 5 6 ) = 6 p 1 < p 2 < p 3 ? p 4 < p 5 ? p 6 p_1<p_2<p_3 \ ? \ p_4<p_5 \ ? \ p_6 p 1 < p 2 < p 3 ? p 4 < p 5 ? p 6 ( 6 3 ) ( 3 2 ) = 60 \binom{6}{3}\binom{3}{2}=60 ( 3 6 ) ( 2 3 ) = 60 p 1 < p 2 < p 3 > p 4 < p 5 > p 6 p_1<p_2<p_3>p_4<p_5>p_6 p 1 < p 2 < p 3 > p 4 < p 5 > p 6 60 − 20 − 6 + 1 = 35 60-20-6+1=35 60 − 20 − 6 + 1 = 35
これを一般化すると、包除原理を用いることで解くことができます。descent set が S S S β n ( S ) \beta_n(S) β n ( S ) S S S α n ( S ) \alpha_n(S) α n ( S )
β n ( S ) = ∑ T ⊆ S ( − 1 ) ∣ S ∖ T ∣ α n ( T )
\beta_n(S)=\sum_{T\subseteq S} (-1)^{|S\setminus T|}\alpha_n(T)
β n ( S ) = T ⊆ S ∑ ( − 1 ) ∣ S ∖ T ∣ α n ( T ) となります。S = { s 1 , s 2 , … , s k } S=\{s_1,s_2,\ldots,s_k\} S = { s 1 , s 2 , … , s k } α n ( S ) \alpha_n(S) α n ( S )
α n ( S ) = ( n s 1 , s 2 − s 1 , … , s k − s k − 1 , n − s k )
\alpha_n(S)=\binom{n}{s_1,s_2-s_1,\ldots,s_k-s_{k-1},n-s_k}
α n ( S ) = ( s 1 , s 2 − s 1 , … , s k − s k − 1 , n − s k n ) と表されます。したがって
β n ( S ) = ∑ 1 ≤ i 1 < ⋯ < i j ≤ k ( − 1 ) k − j ( n s i 1 , s i 2 − s i 1 , … , s i j − s i j − 1 , n − s i j )
\beta_n(S)=\sum_{1\le i_1<\cdots<i_j\le k}(-1)^{k-j}\binom{n}{s_{i_1},s_{i_2}-s_{i_1},\ldots,s_{i_j}-s_{i_{j-1}},n-s_{i_j} \ }
β n ( S ) = 1 ≤ i 1 < ⋯ < i j ≤ k ∑ ( − 1 ) k − j ( s i 1 , s i 2 − s i 1 , … , s i j − s i j − 1 , n − s i j n ) となります。これで descent set が S S S
なお、定義より明らかに
α n ( S ) = ∑ T ⊆ S β n ( T )
\alpha_n(S)=\sum_{T\subseteq S}\beta_n(T)
α n ( S ) = T ⊆ S ∑ β n ( T ) が成り立ちます。
行列式
#
多項係数を書き換えることで、β n ( S ) \beta_n(S) β n ( S )
β n ( S ) = ∑ 1 ≤ i 1 < ⋯ < i j ≤ k ( − 1 ) k − j ( n s i 1 ) ( n − s i 1 s i 2 − s i 1 ) ⋯ ( n − s i j n − s i j )
\beta_n(S)=\sum_{1\le i_1<\cdots<i_j\le k}(-1)^{k-j}\binom{n}{s_{i_1}}\binom{n-s_{i_1}}{s_{i_2}-s_{i_1}}\cdots \binom{n-s_{i_j}}{n-s_{i_j}}
β n ( S ) = 1 ≤ i 1 < ⋯ < i j ≤ k ∑ ( − 1 ) k − j ( s i 1 n ) ( s i 2 − s i 1 n − s i 1 ) ⋯ ( n − s i j n − s i j ) となります。この式から行列式表示
β n ( S ) = det ( ( n − s i s j + 1 − s i ) ) 0 ≤ i , j ≤ k
\beta_n(S)=\det\left(\binom{n-s_i}{s_{j+1}-s_i}\right)_{0\le i,j\le k}
β n ( S ) = det ( ( s j + 1 − s i n − s i ) ) 0 ≤ i , j ≤ k を得ることができます。ただし s 0 = 0 , s k + 1 = n s_0=0, s_{k+1}=n s 0 = 0 , s k + 1 = n n = 6 , S = { 3 , 5 } n=6, S=\{3,5\} n = 6 , S = { 3 , 5 }
β n ( S ) = det ( ( 6 3 ) ( 6 5 ) ( 6 6 ) ( 3 0 ) ( 3 2 ) ( 3 3 ) 0 ( 1 0 ) ( 1 1 ) ) = det ( 20 6 1 1 3 1 0 1 1 ) = 35
\beta_n(S)=\det\begin{pmatrix}
\binom63 & \binom65 & \binom66 \\
\binom30 & \binom32 & \binom33 \\
0 & \binom10 & \binom11
\end{pmatrix}=\det\begin{pmatrix}
20 & 6 & 1 \\
1 & 3 & 1 \\
0 & 1 & 1
\end{pmatrix}=35
β n ( S ) = det ( 3 6 ) ( 0 3 ) 0 ( 5 6 ) ( 2 3 ) ( 0 1 ) ( 6 6 ) ( 3 3 ) ( 1 1 ) = det 20 1 0 6 3 1 1 1 1 = 35 となり、上で求めた数値と一致します。
この行列はほぼ上三角行列の形をしています。通常の行列式計算は時間計算量が O ( n 3 ) O(n^3) O ( n 3 ) O ( n 2 ) O(n^2) O ( n 2 )
LGV 公式
#
行列式表示は LGV (Lindström-Gessel-Viennot) 公式から導くこともできます。
まず LGV 公式の主張を述べます。Γ = ( V , E ) \Gamma=(V,E) Γ = ( V , E ) e ∈ E e\in E e ∈ E w ( e ) ∈ Z w(e)\in \mathbb{Z} w ( e ) ∈ Z P = ( a 1 , … , a n ) P=(a_1,\ldots,a_n) P = ( a 1 , … , a n ) w ( P ) = w ( a 1 , a 2 ) w ( a 2 , a 3 ) ⋯ w ( a n − 1 , a n ) w(P)=w(a_1,a_2)w(a_2,a_3)\cdots w(a_{n-1},a_n) w ( P ) = w ( a 1 , a 2 ) w ( a 2 , a 3 ) ⋯ w ( a n − 1 , a n ) a 1 , … , a n , b 1 , … , b n ∈ V a_1,\ldots,a_n,b_1,\ldots,b_n\in V a 1 , … , a n , b 1 , … , b n ∈ V n × n n\times n n × n
M ( a , b ) = ( ∑ P : a i → b j w ( P ) ) 1 ≤ i , j ≤ n
M(a,b)=\left(\sum_{P\colon a_i\to b_j}w(P)\right)_{1\le i,j\le n}
M ( a , b ) = P : a i → b j ∑ w ( P ) 1 ≤ i , j ≤ n を定めます。ただし和は a i a_i a i b j b_j b j
定理 (LGV): 条件「i 1 < i 2 , j 1 > j 2 i_1<i_2, j_1>j_2 i 1 < i 2 , j 1 > j 2 a i 1 a_{i_1} a i 1 b j 1 b_{j_1} b j 1 a i 2 a_{i_2} a i 2 b j 2 b_{j_2} b j 2
det M ( a , b ) = ∑ ( P 1 , … , P n ) w ( P 1 ) ⋯ w ( P n )
\det M(a,b)=\sum_{(P_1,\ldots,P_n)}w(P_1)\cdots w(P_n)
det M ( a , b ) = ( P 1 , … , P n ) ∑ w ( P 1 ) ⋯ w ( P n ) が成り立つ。ここで和は P i P_i P i a i a_i a i b i b_i b i
条件を仮定しないバージョンもありますが、ここでは扱わないので割愛します。
特に重みがすべて 1 のとき、LGV の右辺は非交差経路の本数になります。これを用いて β n ( S ) \beta_n(S) β n ( S )
順列 ( p 1 , … , p n ) (p_1,\ldots,p_n) ( p 1 , … , p n ) f j f_j f j p i < p j p_i<p_j p i < p j i ( 1 ≤ i < j ) i \ (1\le i<j) i ( 1 ≤ i < j ) p = ( 2 , 5 , 4 , 1 , 3 ) p=(2,5,4,1,3) p = ( 2 , 5 , 4 , 1 , 3 ) f = ( 0 , 1 , 1 , 0 , 3 ) f=(0,1,1,0,3) f = ( 0 , 1 , 1 , 0 , 3 ) f f f 0 ≤ f i ≤ i − 1 0\le f_i\le i-1 0 ≤ f i ≤ i − 1 f f f p p p p i > p i + 1 p_i>p_{i+1} p i > p i + 1 f i ≥ f i + 1 f_i\ge f_{i+1} f i ≥ f i + 1
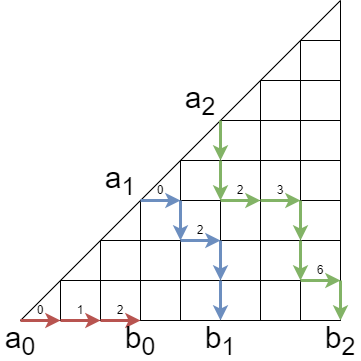
descent set を S = { s 1 , … , s k } S=\{s_1,\ldots,s_k\} S = { s 1 , … , s k } s 0 = 0 , s k + 1 = n s_0=0,s_{k+1}=n s 0 = 0 , s k + 1 = n a i = ( s i , s i ) , b i = ( s i + 1 , 0 ) ( 0 ≤ i ≤ k ) a_i=(s_i,s_i), b_i=(s_{i+1},0) \ (0\le i\le k) a i = ( s i , s i ) , b i = ( s i + 1 , 0 ) ( 0 ≤ i ≤ k ) p p p f f f
上の図は f = ( 0 , 1 , 2 , 0 , 2 , 2 , 3 , 6 ) f=(0,1,2,0,2,2,3,6) f = ( 0 , 1 , 2 , 0 , 2 , 2 , 3 , 6 ) ( i , j ) , ( i + 1 , j ) (i,j),(i+1,j) ( i , j ) , ( i + 1 , j ) i − j i-j i − j f f f
この対応は全単射となることが示せます。まとめると、descent set が S S S β n ( S ) \beta_n(S) β n ( S ) f f f det M ( a , b ) \det M(a,b) det M ( a , b ) a i a_i a i b j b_j b j ( s j + 1 s j + 1 − s i ) \binom{s_{j+1}}{s_{j+1}-s_i\ } ( s j + 1 − s i s j + 1 )
β n ( S ) = det ( ( s j + 1 s j + 1 − s i ) ) i , j
\beta_n(S)=\det\left(\binom{s_{j+1}}{s_{j+1}-s_i}\right)_{i,j}
β n ( S ) = det ( ( s j + 1 − s i s j + 1 ) ) i , j となります。
Aitken の公式
#
さらに Aitken の公式からも行列式表示を導出できます。Aitken の公式は標準タブローの個数を行列式を用いて表す公式です。まず標準タブローについて解説します。
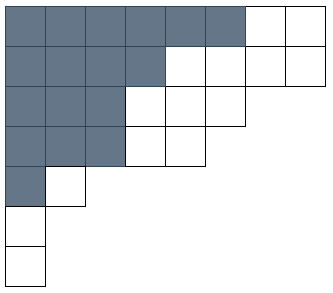
λ = ( λ 1 , λ 2 , … , λ k ) \lambda=(\lambda_1,\lambda_2,\ldots,\lambda_k) λ = ( λ 1 , λ 2 , … , λ k ) λ 1 ≥ λ 2 ≥ ⋯ ≥ λ k ≥ 1 \lambda_1\ge\lambda_2\ge\cdots\ge\lambda_k\ge 1 λ 1 ≥ λ 2 ≥ ⋯ ≥ λ k ≥ 1 i i i λ i \lambda_i λ i λ \lambda λ λ , μ \lambda,\mu λ , μ i i i μ i ≤ λ i \mu_i\le \lambda_i μ i ≤ λ i λ \lambda λ i i i μ i \mu_i μ i λ / μ \lambda/\mu λ / μ
図は λ = ( 8 , 8 , 6 , 5 , 2 , 1 , 1 ) , μ = ( 6 , 4 , 3 , 3 , 1 ) \lambda=(8,8,6,5,2,1,1), \mu=(6,4,3,3,1) λ = ( 8 , 8 , 6 , 5 , 2 , 1 , 1 ) , μ = ( 6 , 4 , 3 , 3 , 1 )
λ / μ \lambda/\mu λ / μ n = ∣ λ / μ ∣ n=|\lambda/\mu| n = ∣ λ / μ ∣ λ / μ \lambda/\mu λ / μ 1 , 2 , … , n 1,2,\ldots,n 1 , 2 , … , n
各行について左から右に単調増加
各列について上から下に単調増加
をみたすものです。
歪ヤング図形 λ / μ \lambda/\mu λ / μ
n ! det ( 1 ( λ i − μ j − i + j ) ! )
n!\det\left(\frac{1}{(\lambda_i-\mu_j-i+j)!}\right)
n ! det ( ( λ i − μ j − i + j )! 1 )
ただし負の整数の階乗の逆数は 0 であるとします。この公式を Aitken の公式と呼びます。
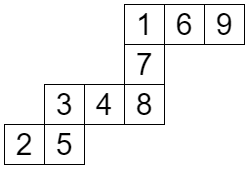
この公式から順列の個数 β n ( S ) \beta_n(S) β n ( S ) S S S
上の図は descent set が S = { 2 , 5 , 6 } S=\{2,5,6\} S = { 2 , 5 , 6 } ( 2 , 5 , 3 , 4 , 8 , 7 , 1 , 6 , 9 ) (2,5,3,4,8,7,1,6,9) ( 2 , 5 , 3 , 4 , 8 , 7 , 1 , 6 , 9 )
S = { s 1 , s 2 , … , s k } , s 0 = 0 , s k + 1 = n S=\{s_1,s_2,\ldots,s_k\}, s_0=0, s_{k+1}=n S = { s 1 , s 2 , … , s k } , s 0 = 0 , s k + 1 = n λ \lambda λ s 1 , s 2 − 1 , s 3 − 2 , … s_1,s_2-1,s_3-2,\ldots s 1 , s 2 − 1 , s 3 − 2 , … μ \mu μ μ i = λ i + 1 − 1 \mu_i=\lambda_{i+1}-1 μ i = λ i + 1 − 1
β n ( S ) = n ! det ( 1 ( s j + 1 − s i ) ! ) 0 ≤ i , j ≤ k = det ( ( n − s i s j + 1 − s i ) ) 0 ≤ i , j ≤ k
\begin{align*}
\beta_n(S) &= n!\det\left(\frac{1}{(s_{j+1}-s_i)!}\right) _ {0\le i,j\le k} \\
&= \det\left(\binom{n-s_i}{s_{j+1}-s_i}\right)_{0\le i,j\le k}
\end{align*}
β n ( S ) = n ! det ( ( s j + 1 − s i )! 1 ) 0 ≤ i , j ≤ k = det ( ( s j + 1 − s i n − s i ) ) 0 ≤ i , j ≤ k が (再び) 得られます。
de Bruijn のアルゴリズム
#
descent set が S S S j j j γ n ( S , j ) \gamma_n(S,j) γ n ( S , j ) S S S β n ( S ) \beta_n(S) β n ( S ) β n ( S ) = ∑ j = 1 n γ n ( S , j ) \beta_n(S)=\sum_{j=1}^n \gamma_n(S,j) β n ( S ) = ∑ j = 1 n γ n ( S , j )
定理 : n − 1 ∉ S n-1\not\in S n − 1 ∈ S
γ n ( S , j ) = ∑ 1 ≤ i < j γ n − 1 ( S , i )
\gamma_n(S,j)=\sum_{1\le i<j}\gamma_{n-1}(S,i)
γ n ( S , j ) = 1 ≤ i < j ∑ γ n − 1 ( S , i ) をみたし、n − 1 ∈ S n-1\in S n − 1 ∈ S
γ n ( S , j ) = ∑ j ≤ i ≤ n − 1 γ n − 1 ( S ∖ { n − 1 } , i )
\gamma_n(S,j)=\sum_{j\le i\le n-1}\gamma_{n-1}(S\setminus\{n-1\},i)
γ n ( S , j ) = j ≤ i ≤ n − 1 ∑ γ n − 1 ( S ∖ { n − 1 } , i ) をみたす。
証明をします。n − 1 ∉ S n-1\not\in S n − 1 ∈ S ( p 1 , … , p n ) (p_1,\ldots,p_n) ( p 1 , … , p n ) S S S j j j p n p_n p n p 1 , … , p n − 1 p_1,\ldots,p_{n-1} p 1 , … , p n − 1 j j j S S S 1 , 2 , … , n − 1 1,2,\ldots,n-1 1 , 2 , … , n − 1 n − 1 ∉ S n-1\not\in S n − 1 ∈ S j j j
累積和
#
Viennot による累積和を用いたシンプルなアルゴリズムを紹介します。
数列 ( a 1 , a 2 , … , a n ) (a_1,a_2,\ldots,a_n) ( a 1 , a 2 , … , a n ) ( 0 , a 1 , a 1 + a 2 , a 1 + a 2 + a 3 , … , a 1 + a 2 + ⋯ + a n ) (0,a_1,a_1+a_2,a_1+a_2+a_3,\ldots,a_1+a_2+\cdots+a_n) ( 0 , a 1 , a 1 + a 2 , a 1 + a 2 + a 3 , … , a 1 + a 2 + ⋯ + a n )
定理 : 初め数列は ( 1 ) (1) ( 1 ) i = 1 , 2 , … , n − 1 i=1,2,\ldots,n-1 i = 1 , 2 , … , n − 1 i ∉ S i\not\in S i ∈ S i ∈ S i\in S i ∈ S S S S β n ( S ) \beta_n(S) β n ( S )
例として n = 6 , S = { 3 , 5 } n=6, S=\{3,5\} n = 6 , S = { 3 , 5 } β n ( S ) = 35 \beta_n(S)=35 β n ( S ) = 35
初めの数列は ( 1 ) (1) ( 1 )
1 ∉ S 1\not\in S 1 ∈ S ( 0 , 1 ) (0,1) ( 0 , 1 ) 2 ∉ S 2\not\in S 2 ∈ S ( 0 , 0 , 1 ) (0,0,1) ( 0 , 0 , 1 ) 3 ∈ S 3\in S 3 ∈ S ( 1 , 1 , 1 , 0 ) (1,1,1,0) ( 1 , 1 , 1 , 0 ) 4 ∉ S 4\not\in S 4 ∈ S ( 0 , 1 , 2 , 3 , 3 ) (0,1,2,3,3) ( 0 , 1 , 2 , 3 , 3 ) 5 ∈ S 5\in S 5 ∈ S ( 9 , 9 , 8 , 6 , 3 , 0 ) (9,9,8,6,3,0) ( 9 , 9 , 8 , 6 , 3 , 0 )
最終的に得られた数列の総和は 9 + 9 + 8 + 6 + 3 + 0 = 35 9+9+8+6+3+0=35 9 + 9 + 8 + 6 + 3 + 0 = 35
正当性は上述の de Bruijn のアルゴリズムにより保証されます。
成瀬のフック長公式
#
Aitken の公式のセクションで説明したように、この問題は歪ヤング図形上の標準タブローの個数を求める問題と同値です。歪でない通常のヤング図形 (すなわち μ = ∅ \mu=\emptyset μ = ∅
n ! det ( 1 ( λ i − i + j ) ! )
n!\det\left(\frac{1}{(\lambda_i-i+j)!}\right)
n ! det ( ( λ i − i + j )! 1 ) となります。通常のヤング図形では行列式以外の方法で標準タブローの個数を求めることができます。その中でも特に有名なものがフック長公式です。
ヤング図形のあるマスに関するフックとは、そのマスの右または下にあるマスからなる集合です (そのマス自身も含む)。
マス ( i , j ) (i,j) ( i , j ) h ( i , j ) h(i,j) h ( i , j )
定理 (フック長公式): ヤング図形 λ \lambda λ
n ! ∏ ( i , j ) h ( i , j )
\frac{n!}{\prod_{(i,j)}h(i,j)}
∏ ( i , j ) h ( i , j ) n !
つまり、すべてのマスについてフック長を計算し、かけあわせて逆数をとり、n ! n! n !
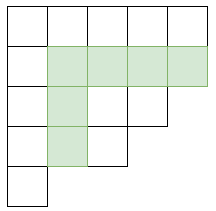
フック長公式の歪ヤング図形への一般化は長らく知られていませんでしたが、成瀬のフック長公式と呼ばれる公式が発見されました。
λ / μ \lambda/\mu λ / μ λ \lambda λ h ( i , j ) h(i,j) h ( i , j ) μ \mu μ
基本操作を何回か行います (0 回でもよい)。こうしてできる盤面について、駒が置かれていないマスのフック長 h ( i , j ) h(i,j) h ( i , j ) ∣ λ / μ ∣ ! |\lambda/\mu|! ∣ λ / μ ∣ ! λ / μ \lambda/\mu λ / μ
定理 (成瀬のフック長公式): λ / μ \lambda/\mu λ / μ E \mathcal{E} E λ / μ \lambda/\mu λ / μ
∣ λ / μ ∣ ! ( ∑ E ∈ E 1 ∏ ( i , j ) h ( i , j ) )
|\lambda/\mu|!\left(\sum_{E\in\mathcal{E}}\frac{1}{\prod_{(i,j)}h(i,j)}\right)
∣ λ / μ ∣ ! ( E ∈ E ∑ ∏ ( i , j ) h ( i , j ) 1 ) ここで ( i , j ) (i,j) ( i , j ) E E E
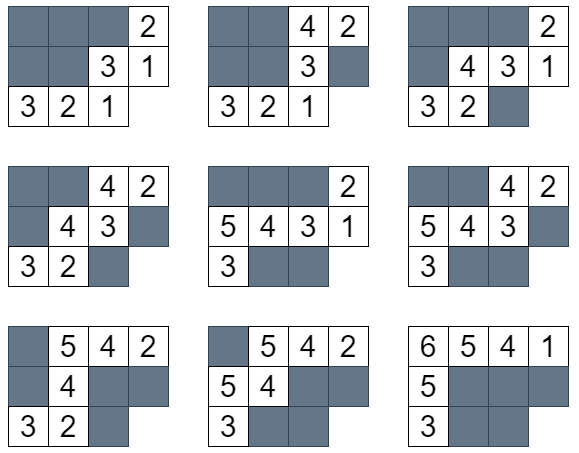
n = 6 , S = { 3 , 5 } n=6,S=\{3,5\} n = 6 , S = { 3 , 5 }
初期の盤面は左上で、基本操作を何回か行って得られる盤面は 9 通りです。それぞれについてフック長の積を求め、逆数を足し合わせて 6 ! 6! 6 !
図を見ると駒の置かれていないマスはジグザグ型になっています。一般に λ / μ \lambda/\mu λ / μ β n ( S ) \beta_n(S) β n ( S )
まとめ
#
EDPC-T Permutation を数学的に深掘りしました。数学の奥深さを感じられたでしょうか。
今後も月刊組合せ論 Natori では様々な組合せ論のトピックを扱っていこうと思います。応援のほどよろしくお願いします!
参考文献
#
Adin, R. M., & Roichman, Y. Enumeration of standard Young tableaux. arXiv:1408.4497 .
de Bruijn, N. G. Permutations with given ups and downs. Nieuw Archief voor Wiskunde, 3/18(1) (1970): 61-65.
Gessel, Ira. & Viennot, Gérard. Binomial determinants, paths, and hook length formulae. Advances in mathematics 58.3 (1985): 300-321.
MacMahon, Percy Alexander 1908II. Second memoir on the compositions of numbers. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 207 65–134.
Marchal, Philippe. Permutations with a prescribed descent set. 2014. hal-00944244.
Morales, Alejandro H., Pak, Igor. & Panova, Greta. Hook formulas for skew shapes I. q-analogues and bijections. Journal of Combinatorial Theory, Series A 154 (2018): 350-405.
Naruse, H. Schubert calculus and hook formula, talk slides at 73rd Sém. Lothar. Combin, Strobl, Austria, 2014; available at https://www.emis.de/journals/SLC/wpapers/s73vortrag/naruse.pdf .
Stanley, Richard P. Enumerative Combinatorics Volume 1 second edition. Cambridge studies in advanced mathematics (2011).
Viennot, Gérard. Permutations ayant une forme donnée. Discrete Mathematics 26.3 (1979): 279-284.
【競技プログラミング】難問も解ける!Young tableaux及びSkew tableauxのフック長の公式と数え上げ問題への適用