↓メインコンテンツへスキップ
組合せ論、楽しい！

【くみあラボ】至高のアルゴリズム、RSK 対応を解説します！【ヤング図形 5】

目次

みなさん、combanwa～！組合せ論系 VTuber の早稲くみあです！

昨日はバレンタインデーでしたね。当日はチョコづくり配信をしていました。見に来てくださった方、ありがとうございました！ちょっと失敗しちゃいましたけど、楽しかったです！

ところで、板チョコってヤング図形みたいですよね？というわけで今回も、ヤング図形の魅力を語っていきますよ～！

まずはプラクティックモノイドの復習から #

前回の記事でプラクティックモノイドを定義しました。2 つの半標準ヤングタブローのかけ算を定義できるという内容でした。

【くみあラボ】ヤングタブローのかけ算！？【ヤング図形 4】

タブロー P の作り方 #

RSK 対応の前に RS 対応、つまりロビンソン・シェンステッド対応を説明します。

RS 対応は順列 $x=(x_1,\ldots,x_n)$ から 2 つの標準ヤングタブローを作る方法です。これは一対一対応になります。

まず 1 つ目のタブロー $P$ を作ります。それは、これです！

$$ P=\boxed{x_1}\cdot \boxed{x_2}\cdots \boxed{x_n} $$

ここで $\boxed{x_1}$ というのは $x_1$ が書かれた 1 マスだけからなるタブローです。順列 $(x_1,\ldots,x_n)$ から 1 マスだけのタブローを $n$ 個作って、順番にかけていくことで $P$ ができます。

試しに $x=(2,4,3,6,5,1)$ で試してみましょう。

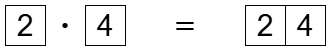
image
image
image
image
image

タブロー Q の作り方 #

タブロー $P=\boxed{x_1}\cdot \boxed{x_2}\cdots \boxed{x_n}$ の計算例を先ほど見ました。順番にかけていくことでタブローを作っていたんですが、書いてある数字を忘れて形だけに注目してみます。

連載の最初の記事で「標準ヤングタブローというのは、ヤング図形の成長記録です。」と書いたように、この成長記録をタブローとして見るのは大事なんです。このタブローこそが、タブロー $Q$ です！

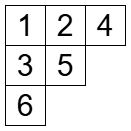
image

こうして 2 つのタブロー $P,Q$ ができました。RS 対応は順列 $x$ から組 $(P,Q)$ を得る操作のことです。RS 対応の性質を紹介します。どれをとっても不思議で、奇跡のように見えてしまいます。

定理

  1. RS 対応は、長さ $n$ の順列の集合と、サイズ $n$ の同じ形をもつ 2 つの標準ヤングタブローの組との間の一対一対応である。
  2. $x$ に対応するタブローの組が $(P,Q)$ のとき、$x$ の逆順列に対応するタブローの組は $(Q,P)$ である。
  3. $x$ の最長増加部分列の長さは、$P,Q$ の一行目の長さに等しい。
  4. $x$ の最長減少部分列の長さは、$P,Q$ の一列目の長さに等しい。

挿入を使った解釈 #

タブロー $P$ を計算するとき、タブロー $T$ に 1 マスだけのタブローをかけた $T\cdot\boxed{x}$ を計算する場面がよく出てきましたね。これがどんなふうになっているか見てみましょう。

$T$ が

12234
234
3

のとき、$T\cdot\boxed{2}$ は

12224
233
34

です。タブロー $T$ のワードは 3|234|12234 です (わかりやすさのために縦棒を入れています)。このワードの右端に 2 を加えて、クヌース同値で変換していきます。クヌース同値とはこのような変換で移り合う関係でした。

  • $x<y\le z$ のとき、$yzx$ を $yxz$ にできる。
  • $x\le y<z$ のとき、$xzy$ を $zxy$ にできる。

では実際にやっていきましょう！

122342 -> 122324 -> 123224 -> 132224 -> 312224

これは「$\text{(古い 1 行目)}\cdot x=y\cdot\text{(新しい 1 行目)}$」ととらえられます。どのような $y$ が出てくるでしょうか。

それは、$x$ より大きい要素のうち最も左端のものです。

というわけで、$T\cdot\boxed{x}$ の計算は次のようなアルゴリズムで説明できます。

  • $T$ の 1 行目から、$x$ より大きい要素のうち最も左端のものを $y$ とする。$y$ のある位置に $x$ を置く。
  • $T$ の 2 行目から、$y$ より大きい要素のうち最も左端のものを $z$ とする。$z$ のある位置に $y$ を置く。
  • もし $z$ より大きい要素がなければ、3 行目の末尾に $z$ を置く。

これをシェンステッドのアルゴリズムといいます。RS 対応をこれで定義する文献が多いですね。

クヌース同値はミクロなものの見方でしたが、それをマクロに捉えたといえますね。なお実際には順番が逆で、シェンステッドのアルゴリズムが先にあってその後にクヌース同値が生まれました。

Viennot の影 #

RS 対応の別の見方として、Viennot の geometric construction と呼ばれるものがあります。

実際に遊んでみてください！

https://www.integral-domain.org/lwilliams/Applets/Math/Viennot.php

ついに RSK 対応の登場です！ #

RS 対応では $x$ を順列にしていましたが、一般の数列にしても大丈夫です。この場合、$Q$ は標準ヤングタブローのままですが、$P$ は半標準ヤングタブローになります。

では $Q$ も半標準ヤングタブローになるような対応はないのかな？と考えたくなりますね。それこそが、RSK 対応です！

RSK 対応では順列や数列の代わりに、成分が非負整数の行列が登場します。

$$ \begin{pmatrix} 0 & 2 & 1 \\ 1 & 1 & 0 \\ 2 & 3 & 1 \end{pmatrix} $$

行列が置換行列のとき、RSK 対応は上で紹介した Viennot の方法と同じになります。フルトンの『ヤング・タブロー』には「行列と玉の方法」というアルゴリズムが載っていて、これは Viennot の方法を一般の行列に拡張したものとなっています。

RSK 対応の詳細を書きたいところですが、時間が足りなくなってきたので割愛させてください。

奇跡 #

今では様々な分野で RSK 対応が研究されています。RSK 対応の亜種や一般化も考えられています。

そんな RSK 対応は、奇跡だという人がいます。

What matters is that each RSK appearance is a shadow of one fundamental result that is yet to be formalized. This suggests we treat RSK as the one true miracle which causes much of what we consider magical about the symmetric group.

(Igor Pak. WHAT IS A COMBINATORIAL INTERPRETATION?)

世界には不思議なことがいっぱいありますよね。なぜ生命があるのか。なぜ宇宙が生まれたのか。私にとっては、なぜ RSK 対応があるのかが不思議です。

RSK 対応には 2 つのタブローの組が出てきましたけど、素人的考えで 3 つ以上のタブローを考えたくなります。でもこれはいい性質がないみたいです。

このことを箱星さんに話したところ、こんなエピソードを紹介してくれました。J. H. コンウェイという数学者は、モンスターという群について「死ぬまでにはモンスターが存在する理由を理解したい」と言っていたそうです。モンスターは有限単純群の中で散在型と呼ばれるクラスに属する群で、散在型の群の中で最も位数が大きい群ですね。そのような群があるだけでも不思議なのに、「ムーンシャイン」というさらに不思議な現象もあります。どうしてこのような不思議な群が存在するのか、コンウェイは理解したかったのでしょう。残念ながらコンウェイはコロナ禍の中で亡くなってしまいました。今後コンウェイの夢を叶える研究が出てくるかもしれません。私も何か貢献したいですが、今の私ではモンスターの足元にも及びません……。

話がそれてしまいましたが、RSK 対応も不思議です。この不思議さに感謝ですね。

おわりに #

というわけで、至高を超えて奇跡のアルゴリズム、RSK 対応を紹介しました！

厳密な定義は時間がなくて紹介できなくてごめんなさい！

いよいよ次回はヤング図形に関する連載の最終回です！楽しい話題をお届けできればと思います。

以上、早稲くみあでした！bye-jection！