【くみあラボ】ヤングタブローのかけ算！？【ヤング図形 4】
目次
みなさん、あけましておめでとうございます！組合せ論系 VTuber の早稲くみあです！
大学院生になると新年もゆっくりできなくて大変ですね～。でも、初詣はちゃんと行ってきましたよ！みなさんはどうでしたか？よかったらコメントください！
ヤングタブロー #
今回の主役もヤングタブローです。特に半標準ヤングタブローを考えます。この記事では、タブローといったら半標準ヤングタブローのことだとします。
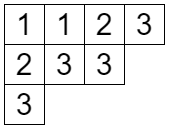
2 つのヤングタブローがあったとき、かけ算ができる！というのが今回の記事のメインです。
かけ算といえば普通は数のかけ算です。数のかけ算しか知らなかった人が、初めて他のかけ算に触れるのは行列ではないでしょうか。行列でもかけ算ができると知って、しかも数のかけ算では当たり前だった交換法則 ($AB=BA$) が成り立つとは限らないと知って驚いた人もいるかもしれません。
現代数学ではいろいろなものがかけ算できます。ヤングタブローもその 1 つです。どうですか？ワクワクしてきませんか？
このワクワクを追いかける旅を一緒にしていきましょう！
タブローのワード #
タブローからワードを作りましょう。ワードというのはタブローに書き込む数字を横一列に並べたもので、今回の場合は数列と同じだと思ってもよいです。
タブローに書かれている数字を「左から右へ、下から上へ」読んでいきます。上の図の場合は 3,2,3,3,1,1,2,3 になります。カンマは省略して 32331123 と書くこともあります。
ワードの連結とタブローのかけ算 #
2 つのタブローがあったとき、このようにワードを作って、連結します。例えば 2 つのタブロー
113 12
2 33
からワードを作って連結すると、21133312 になります。ですがこれはタブローから得られるワードではありません。先ほどの 32331123 であれば 3|233|1123 のように減少するところで区切れば復元できますが、21133312 の場合 2|11333|12 となり、これを組み立ててもタブローにはなりません。
そこで、ワードを変形して、タブロー由来のワードになるようにすることを考えるんです。
変形のルールは 2 つです。
- $x<y\le z$ のとき、$yzx$ を $yxz$ にできる。
- $x\le y<z$ のとき、$xzy$ を $zxy$ にできる。
例えば 331 を 313 にできるので、21133312 を 21133132 にできます。これを繰り返すと、23311123 にできます。（確かめてみましょう！）
この 23311123 は
11123
233
というタブローから得られるワードです。
そこで、こんなかけ算を定義します。
113 * 12 = 11123
2 33 233
これがタブローのかけ算です！
深掘り #
これまでの流れをまとめると
- 2 つのタブローからワードを得る
- 連結する
- 変形を繰り返してタブロー由来のワードを得る
- このタブローをかけ算の答えとする
ということになりますが、気になるところがいくつかありますよね。
- 必ずタブロー由来のワードが得られるの？
- それは一通りなの？
実は大丈夫なんです。このような定理があります。
クヌース同値という用語を説明していませんでしたが、あるワードから先ほどの変形を繰り返してワードを作ったとき、2 つのワードはクヌース同値といいます。
この定理の証明は簡単ではないんですが、この連載のコンセプトは「組合せ論の楽しい部分を散策する」なので、証明は省略します。気になる人は参考文献を見てみてください。
かけ算が無事定義できました。しかもこんな性質をみたします。
両辺とも $T_1,T_2,T_3$ から得られるワードを連結して、それと対応する一意的なタブローに等しいことから、この定理は簡単にわかりますね。
というわけで、タブローのかけ算は結合法則をみたします！さらに空っぽの図形が単位元になります。結合法則をみたして単位元をもつ代数系をモノイドといいます。タブローにはモノイドの構造が入るということですね。このモノイドを、プラクティックモノイドといいます。
プラクティックって不思議な響きですよね。聞いたことがない言葉なので調べてみたんですが、一説によるとプレートテクトニクスに由来する言葉だそうです。聞くだけでワクワクするような専門用語ってありますよね。とある数学マンガにはこんなセリフがありました。
名前の良さは大事です。事実、数学科生の9割は名前のかっこよさで専攻分野を選んでいます。 (出典: https://x.com/goteten_math/status/1873195467733135765)
組合せ論を布教するためには、組合せ論のかっこいい言葉をアピールする必要がありそうですね。extremal combinatorics (極値組合せ論) とかどうですか？今度こういう言葉を集めて動画にしてみたいです！
プラクティックモノイドも、名前の不思議さに魅力を感じられそうですね。つかみどころがなさそうな名前に、もっと知りたいという気持ちを感じませんか？
暗号への応用？ #
プラクティックモノイドについて調べていたら、暗号への応用も考えられていることを知りました。
暗号にはいろいろな種類があります。例えば、共通鍵暗号があります。アリスとボブの 2 人が秘密のやりとりをするために共通の鍵を使う方法ですけど、どうやって共通の鍵を決めるかという問題があります。有名なものにはディフィー・ヘルマン鍵共有というものがありますが、それはこのようなものです。
- 大きな素数 $p$ と、$p$ 未満の整数 $x$ を決めて、共有する。
- アリスは 2 以上 $p$ 未満の秘密の整数 $a$ を決める。これは秘密にする。
- ボブも 2 以上 $p$ 未満の秘密の整数 $b$ を決める。これも秘密にする。
- アリスは $A=x^a\bmod{p}$ を計算し、ボブに送る。
- ボブは $B=x^b\bmod{p}$ を計算し、アリスに送る。
- アリスは受け取った $B$ をもとに $K_A=B^a\bmod{p}$ を計算する。
- ボブは受け取った $A$ をもとに $K_B=A^b\bmod{p}$ を計算する。
- $(x^a)^b=(x^b)^a$ であることから $K_A=K_B$ となるので、これを共通鍵とする。
ここで、$a,b$ は秘密ですが、$A,B,p,x$ は送信しているので第三者に聞かれているかもしれません。もしあなたが第三者で、傍受した $A,B,p,x$ から共通鍵 $K_A(=K_B)$ を知りたいとしましょう。そのためには秘密の $a,b$ を計算しないといけません。すると、$A=x^a\bmod{p}$ をみたす $a$ を求めたくなります。もし $A,x,a$ が実数で $\bmod{p}$ を無視すれば、 $a=\log_xA$ のように対数になります。しかし $\bmod{p}$ で考えているということが大事で、この場合対数の計算は難しくてとても時間がかかります。これを離散対数問題といいます。離散対数問題の計算が難しいということが、ディフィー・ヘルマン鍵共有の安全性を支えています。
しかし、現代ではコンピュータの性能も上がっていますし、量子コンピュータという新しいものも開発されています。そうすると離散対数問題もあっさり解かれてしまうようになるかもしれません。
そこで、新しい鍵共有の方法が必要になるわけです。その 1 つとして、プラクティックモノイドが使えるのではないかという提案がされました。それはこのようなものです。
- アリスとボブはプラクティックモノイドの元（つまりタブロー）$g$ を決めて共有する。
- アリスはタブロー $a$ を決めて秘密にする。$A=ag$ をボブに送る。
- ボブはタブロー $b$ を決めて秘密にする。$B=gb$ をアリスに送る。
- アリスは $K_A=aB$ を計算し、ボブは $K_B=Ab$ を計算する。
- 結合法則より $(ag)b=a(gb)$ なので $K_A=K_B$ である。
この手法が安全かどうかは、離散対数問題に対応する問題、つまり $g,A,B$ がわかったときに $a,b$ を簡単に求められるかどうかにかかっています。
残念ながら、この問題はある程度の速さで解けてしまうようです。もし難しい問題だったら、暗号の世界にヤング図形が使われる楽しい世界が来るかも！と期待していたんですけどね……。
ちなみに、お気づきの方もいるかもしれませんが、この方法はプラクティックモノイドに限らず一般のモノイドでできます。プラクティックモノイドの亜種がいろいろ知られているので、対応する問題を考えてみるのも面白いかもしれません。こういうところから研究は始まります！
おわりに #
今回はヤングタブローがかけ算できるということを紹介しました。
紹介しきれませんでしたが、バンプやスライドというアルゴリズムを使ってプラクティックモノイドを調べることもできます。
次回の記事では、そういったヤングタブローのアルゴリズムについて紹介していきたいと思います！あのアルゴリズムも登場するかも……？
以上、早稲くみあでした！bye-jection！
参考文献 #
- W. Fulton (池田岳・井上玲・岩尾慎介 訳), ヤング・タブロー ―表現論と幾何への応用―, 丸善出版, 2019.
- Brown, Daniel R. L. Plactic key agreement (insecure?). J. Math. Cryptol. 17, (2023).
- Monico, Chris. Division in the plactic monoid. J. Algebra Appl. 23, No. 7, (2024).